- линейчатая поверхность, прямолинейные образующие к-рой параллельны одной и той же плоскости. Ее стрикционная линия плоская. Радиус-вектор К. п.: r=p(u)+vl(u), причем 
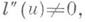(l, l', l')=0. Если все образующие К. п. пересекают одну и ту же прямую, то она является коноидом.
Лит.:[1] Catalan E., Memoire sur les surfaces gauches a plan directeur, P., 1843.
И. Х. Сабитов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
Поверхность Каталана — Поверхность Каталана линейчатая поверхность, прямолинейные образующие которой параллельны одной и той же плоскости. Её стрикционная линия плоская. Радиус вектор поверхности Каталана: , причем . Если все образующие поверхности Каталана… … Википедия
ЛИНЕЙЧАТАЯ ПОВЕРХНОСТЬ — в дифференциальной геометрии поверхность, образованная движением прямой линии. Прямые, принадлежащие этой поверхности, называются прямолинейными образующими, а каждая кривая, пересекающая все прямолинейные образующие, направляющей кривой. Если… … Математическая энциклопедия
Линейчатая поверхность — Линейчатый геликоид … Википедия
КОНОИД — Каталана поверхность, все прямолинейные образующие к рой пересекают фиксированную прямую ось К. Напр., гиперболич. параболоид есть К. с двумя осями. Радиус вектор К. где {a, b, g} единичный вектор, имеющий направление оси К., f(и) некоторая… … Математическая энциклопедия
Испанская кухня — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей … Википедия
