НЕПРИВОДИМОЕ АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО

- аналитическое пространство, к-рое нельзя представить в виде объединения локально конечного семейства его аналитич. одпространств. Н. а. п. является обобщением понятия неприводимого аналитического множества. Всякое аналитич. ространство можно единственным образом представить в виде несократимого объединения локально конечного семейства его неприводимых аналитич. одпространств, называемых его неприводимыми компонентами (разложение пространства на неприводимые компоненты). Комплексное аналитич. многообразие неприводимо тогда и только тогда, когда оно связно; неприводимые компоненты многообразия - это его компоненты связности. Росток аналитич. ространства в данной его точке наз. неприводимым, если его нельзя представить в виде объединения конечного числа ростков аналитич. одпространства в этой же точке. Всякий росток аналитич. ространства в точке единственным образом представляется в виде объединения конечного числа своих неприводимых подростков. 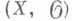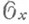Росток приведенного комплексного пространства в точке неприводим тогда и только тогда, когда локальное кольцо не имеет делителей нуля. Комплексное пространство, ростки к-рого во всех его точках неприводимы, является неприводимым тогда и только тогда, когда оно связно; неприводимые компоненты такого пространства суть его компоненты связности.

Лит.:[1] Ганнинг. Р., Росси X., Аналитические функции многих комплексных переменных, пер. с англ., М., 1969; [2] Эрве М., Функции многих комплексных переменных. Локальная теория, пер. с англ., М., 1965.