ИТЕРАЦИОННЫЙ АЛГОРИТМ

- рекурсивный алгоритм, реализующий в нек-ром топологич. пространстве Vпоследовательность точечно-множественных отображений A_k: V-> V, при помощи к-рых по начальной

точке вычисляют последовательность точек согласно формулам

Операцию (1) наз. итерацией, а последовательность u^k- итерационной последовательностью.

И. а. (или методы последовательных приближений) применяют как для нахождения решения операторного уравнения

или минимума нек-рого функционала, или собственных значений и элементов уравнения Au=luи т. п., так и для доказательства существования решений этих задач. И. а. (1) наз. сходящимся при начальном приближении и ⁰ к решению иупомянутых задач, если

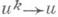при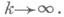

Операторы A_k для решения уравнения (2), заданного в линейном метрич. пространстве V, обычно строят по формулам

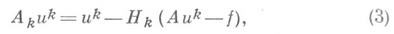
где H_k(V->V)- некоторая, определяющая тип И. а., последовательность операторов. В основе построения И. а. типа (1), (3) лежат или сжатых отображений принцип и его обобщения, или вариационные методы минимизации нек-рого связанного с задачей функционала. При этом используются различные методы построения операторов A_k, напр, варианты Ньютона метода, или спуска метода. Операторы Н _k стараются выбрать так, чтобы быстрая сходимость u^k к иобеспечивалась при условии, что численная реализация операции A_ku^k при заданном объеме памяти ЭВМ была достаточно проста, нетрудоемка по количеству операций и "устойчива к ошибкам округления.

Хорошо разработаны и исследованы И. а. решения линейных задач. И. а. делятся при этом на линейные и нелинейные. К линейным относятся, напр., Гаусса метод, Зейделя метод, верхней релаксации метод, И. а. с чебышевскими параметрами; к нелинейным - вариационные методы: наискорейшего спуска метод, сопряженных градиентов метод, минимизации невязок метод и т. д. Одним из эффективных И. а. является метод с использованием чебышевских параметров, когда А- самосопряженный оператор со спектром на отрезке [ т, М], где М>m>0. Этот метод дает оптимальную (при данной информации о границах спектра) оценку сходимости на заранее задаваемом N-м шаге. Записывается метод в виде

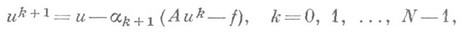
где

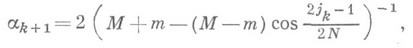
N-ожидаемое число итераций, в нем используется x_N=(j₁, j₂, ..., j_N)- специальная перестановка N-гo порядка, хорошо перемешивающая для устойчивости счета корни многочлена Чебышева. Для N=2ⁿ перестановку x_N можно построить, напр., так: х ₂=(1, 2), и если известна перестановка х ₂i-1= (j₁, j₂, ..., i₂i-1), то х ₂i=(j₁, 2ⁱ+1-j₁, j₂, 2ⁱ+1-j₂, ...). При N=16 эта перестановка имеет вид: (1, 16, 8, 9, 4, 13, 5, 12, 2, 15, 7, 10, 3, 14, 6, 11).

Существуют И. а., использующие rпредыдущих приближений и ^k, u^k-1, ..., u^k-r+1;они наз. r-шаговыми и обладают повышенной скоростью сходимости.

И. а. широко применяются при решении многомерных задач математич. физики, для нек-рых классов таких задач существуют специальные быстросходящиеся И. а. Напр., переменных направлений метод, метод, изложенный в [7] для эллиптических краевых задач, нек-рые методы для задач переноса частиц или излучений (см. [1] - [7]).

Лит.:[1] Канторович Л. В., Авилов Г. П., Функциональный анализ, 2 изд., М., 1977; [2] Коллатц Л., Функциональный анализ и вычислительная математика, пер. с нем., М., 1969; [3] Марчук Г. И., Лебедев В. И., Численные методы в теории переноса нейтронов, М., 1971; [4] Бахвалов Н. С, Численные методы, 2 изд., М., 1975; [5] Красносельский М. А. и др., Приближенное решение операторных уравнений, М., 1969; [6] Лебедев В. И., в кн.: Тр. института кибернетики АН УССР, К., 1972, с. 109- 135; [7] Федоренко Р. П., "Успехи матем. наук", 1973, т. 28, в. 2, с. 121 - 82.

В. И. Лебедев.