ИСКЛЮЧЕНИЯ ТЕОРИЯ

- теория исключения неизвестных из системы алгебраич. уравнений. Более точно, пусть имеется система уравнений

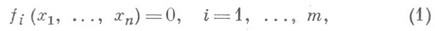
где f_i - многочлены с коэффициентами из заданного поля Р. Задача исключения неизвестных х ₁ ,..., х _k из системы (1) (неоднородная задача теории исключения) может быть сформулирована следующим образом: найти проекцию множества решений системы (1) на пространство координат х _k+1, ..., х _п. В том случае, когда каждое из уравнений однородно по совокупности неизвестных х ₁, . .., х _k, рассматривается также однородная задача теории исключения (неоднородная задача в этом случае тривиальна): найти проекцию на пространство координат х _k+1,..., х _п множества тех решений системы (1), в к-рых не все неизвестные x₁, ..., x_k равны нулю.

Неоднородная задача И. т. может также трактоваться как нахождение условий на коэффициенты системы алгебраич. уравнений, при к-рых эта система совместна, а однородная задача' И. т.- как нахождение условий на коэффициенты , системы однородных алгебраич. уравнений, при к-рых эта система имеет ненулевое решение.

Основные результаты И. т. заключаются в том, что если поле Ралгебраически замкнуто, то решение однородной задачи И. т. является алгебраическим множеством, т. е. множеством решений системы алгебраич. уравнений, а решение неоднородной задачи - конструктивным множеством в смысле алгебраич. геометрии, т. е. конечным объединением множеств вида где Ми Nсуть алгебраич. множества. В нек-рых простейших случаях решение задач И. т. известно в явном виде.

1) Пусть рассматриваемая система уравнений линейна и однородна относительно х ₁,..., х _k, т. е. имеет вид

где а _ij- многочлены от x_k+1, ..., х _п. При заданных значениях х _k+1, . .., х _п система (2) имеет ненулевое решение тогда и только тогда, когда ранг матрицы А= (я/у) меньше к(см. Линейное уравнение). Решением однородной задачи И. т. в этом случае будет множество в пространстве координат X_k+1,. . ., х _п, выделяемое условиями равенства нулю всех миноров порядка кматрицы А.

2) Пусть рассматриваемая система уравнений линейна относительно х ₁, ..., х _k, т. е. имеет вид

где a_ij, b_i - многочлены от х _k+1,. . ., х _п. Пусть 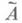- матрица, получаемая приписыванием к матрице А=(a_ij )столбца (b_i). При заданных значениях х _k+1,..., х _п система (3) совместна тогда и только тогда, когда ранг матрицы Аравен рангу матрицы А. Следовательно, результатом исключения x₁, ..., х _п из системы (3) является где M_r- множество точек (x_k+1, ..., х _п), в к-рых а N_r- множество точек, в к-рых rkА<r (множества M_r и N_r алгебраические).

3) Пусть k=2, поле Ралгебраически замкнуто и рассматриваемая система состоит из двух уравнений, однородных по х ₁, х ₂:

где а ₀, a₁, . . ., а _п, b₀, b₁,. .., b _т- многочлены от х ₃, ..., x_n. При заданных значениях х ₃,. . ., х _п система (4) имеет ненулевое решение тогда и только тогда, когда равен нулю результант

Это и дает решение однородной задачи И. т. в рассматриваемом случае.

4) Пусть к=1, поле Ралгебраически замкнуто и рассматриваемая система состоит из двух уравнений:

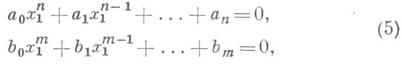
где а ₀, a₁, ..., а _п, b₀, b₁, ..., b _т- многочлены от х ₂, . .., х _п. При заданных значениях х ₂,..., х _п, не обращающихся в нуль а ₀ или b₀, система (5) совместна тогда и только тогда, когда

Если же а ₀=b₀=0, то следует рассмотреть

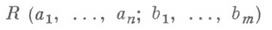
и т. д. Это позволяет описать в явном виде результат исключения х ₁ из системы (5).

Исключение неизвестных из произвольной системы алгебраич. уравнений может быть проведено последовательно (т. е. исключается сначала одно неизвестное, затем другое и т. д.) при помощи описываемых ниже "элементарных преобразований". Поскольку после исключения одного неизвестного получается, вообще говоря, не алгебраическое, но конструктивное множество, то следует рассмотреть задачу проектирования на пространство координат х ₂,..., х _п произвольного конструктивного множества в Р ^п.

Всякое конструктивное множество может быть представлено как объединение множеств решений совокупности систем алгебраич. уравнений и неравенств. (Под алгебраич. неравенством здесь понимается неравенство вида где f - многочлен.) Элементарным преобразованием такой совокупности наз. преобразование одного из следующих типов: в одной из систем к одному из уравнений прибавляется другое, умноженное на многочлен; в системе, содержащей неравенство f неравно0, одно из уравнений умножается на f; в одной из систем к одному из неравенств прибавляется одно из уравнений, умноженное на многочлен; одна из систем заменяется на две, получаемые из нее приписыванием уравнения f=0и неравенства f неравно 0 соответственно (f - нек-рый многочлен); в одной из систем два неравенства заменяются их произведением.

Элементарные преобразования не изменяют объединения множеств решений систем, входящих в данную совокупность. Применяя элементарные преобразования, можно привести любую совокупность систем алгебраич.

уравнений и неравенств с неизвестными х ₁, ..., х _п к такому виду, когда в каждую из систем входит не более одного уравнения или неравенства, содержащего х ₁ , причем наряду с таким уравнением f=0 или неравенством 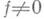в эту же систему входит неравенство где f₀ - многочлен от x₂, ..., х _п, являющийся старшим коэффициентом в разложении f по степеням х ₁. Если поле Ралгебраически замкнуто, то, отбросив в системах полученной совокупности уравнения и неравенства, содержащие х ₁, получают совокупность систем алгебраич. уравнений и неравенств с неизвестными х ₂,...., х _п, к-рая и задает проекцию множества Xна пространство координат х ₂,..., х _п.

Последовательное исключение неизвестных с помощью элементарных преобразований позволяет в принципе свести решение произвольной системы алгебраич. уравнений с пнеизвестными к решению ряда алгебраич. уравнений с одним неизвестным.

Лит.:[1] Ходж В., Пидо Д., Метод алгебраической геометрии, пер. с англ., т. 1, М., 1954; [2] Ван-дер-Варден Б. Л., Алгебра, пер. с нем., М., 1976.

Э. Б. Винберг.