ИНВАРИАНТНОСТЬ СТАТИСТИЧЕСКОЙ ПРОЦЕДУРЫ

- эквивариантность (см. ниже) какого-либо решающего правила в статистич. задаче, постановка к-рой допускает группу Gсимметрии, относительно этой группы G. Понятие И. с. п. возникает в первую очередь в так наз. параметрич. задачах математич. статистики, когда имеется априорная информация: распределение вероятностей Р(dm )исходов ш наблюдений принадлежит известному семейству {Р_q ,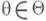}. Говорят, что статистич. проблема решения G-э квивариантна относительно группы Gизмеримых преобразований gизмеримого пространства (W, B_W). исходов, если выполнены условия: 1) существует гомоморфизм f группы Gна нек-рую группу Gпреобразований пространства в параметров со свойством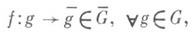

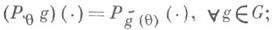
2) существует гомоморфизм hгруппы Gна нек-рую группу Gизмеримых преобразований измеримого пространства (D, В _D) решений d,

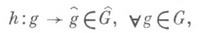
со свойством

где L(Q, d)- функция потерь; 3) вся дополнительная априорная информация о возможных значениях параметра (априорная плотность р(0), разбиение на альтернативы Q=QЪ ... ЪQ_s и т. п.) G-инвариантна или G-эквивариантна. При этих условиях решающее правило d : безразлично детерминированное или рандомизированное, наз. инвариантной (точнее G-э квивариантной) процедурой, если

Риск

эквивариантной решающей процедуры d является G-инвариантом, в частности он не зависит от q, если группа Gдействует на в транзитивно.

Как правило, в параметрич. задачах не существует гарантированно наилучшей решающей процедуры, к-рая минимизировала бы риск при каждом значении параметра В частности, процедура может приводить к очень малым значениям риска для нек-рых 6 за счет ухудшения качества при других априори столь же возможных значениях параметра. Эквивариантность в какой-то степени обеспечивает беспристрастность подхода. Когда группа Gдостаточно богата, существует оптимальная инвариантная процедура с равномерно наименьшим среди инвариантных процедур риском.

Инвариантные процедуры широко применяются в проверке гипотез (см. также Инвариантный критерий )и в оценивании параметра закона распределения. Так, в задаче оценки неизвестного вектора средних для семейства m-мерных нормальных законов

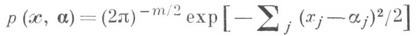
с единичной матрицей ковариаций и гауссовой функцией потерь 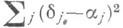оптимальной эквивариантной оценкой будет обычное выборочное среднее

Группой Gздесь служит произведение группы S_N перенумерации наблюдений и группы Ort (m) движений евклидова пространства R^m;. При 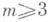в задаче существуют неэквивариантные оценки, приводящие к меньшему, чем у х*, риску при всех a, однако область существенной "сверхэффективности" оказывается незначительной и безгранично уменьшается с ростом объема Nвыборки. Возможность сверхэффективных процедур связана с некомпактностью G.

Эквивариантные статистич. процедуры возникают также в ряде непараметрич. задач статистики, когда априорное семейство распределений Рисходов существенно бесконечномерно, а также при построении доверительных множеств ,для параметра 0 распределения при наличии мешающих параметров.

Лит.:[1] Леман Э., Проверка статистических гипотез, пер. с англ., М., 1964.

Н. Н. Ченцов.