ДИОФАНТОВЫХ ПРИБЛИЖЕНИЙ ПРОБЛЕМЫ ЭФФЕКТИВИЗАЦИИ

- получение эффективных решений задач диофантовых приближений, для к-рых известно решение, полученное неэффективными методами, т. е. методами, не допускающими принципиальной возможности численного выражения результата. Таковы, например, теоремы А. Туэ (A. Thue), К. Зигеля (С. Siegel), К. Рота (К. Roth), В. Шмидта (W. Schmidt), их обобщения, аналоги и следствия (см. Туэ- Зигеля - Рота теорема, Диофантовы приближения). Неэффективность этих теорем объясняется логич. структурой метода, основанного на предположении о существовании объектов, не определяемых конструктивно. Так, в случае рациональных приближений к алгебраич. числам граница для знаменателей "хороших" приближений, устанавливаемая в процессе рассуждений, зависит от одного из этих "хороших" приближений, существование к-рого не доказывается.

Эффективное решение задачи часто представляет большие трудности. Лишь недавно удалось получить эффективное усиление неравенства Лиувилля (см. Лиуеилля число). Метод доказательства существенно отличается от метода Туэ - Зигеля - Рота и связан с привлечением эффективных методов теории трансцендентных чисел (см. Линейная форма от логарифмов алгебралч. чисел). Наилучший известный результат (1978) имеет вид

где а - алгебраич. число степени n>3, x>0, у- целые рациональные, с>0 и d>0 определяются в явном виде через a (см. [3]). Это неравенство далеко от своего неэффективного аналога: вместо показателя - n+1 +d неэффективные методы дают -1 -e с любым e>0, но с неизвестной функцией сот a и e. Доказательство эффективного неравенства

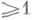с функцией a(n), растущей, напр., как п ^e., представляет большой интерес в связи с нахождением границ решений диофантова уравнения где многочлен f(x, у )определяет кривую рода (конечность числа решений доказана в 1929 К. Зигелем, использовавшим неэффективные оценки, см. Диофантова геометрия).

Несмотря на то, что эффективные оценки получаются значительно хуже неэффективных, знание их зависимости от параметров задачи позволяет устанавливать новые результаты, недоступные неэффективным методам. Так, эффективные оценки линейных форм от логарифмов алгебраических чисел позволили Туэ найти оценки решений многих диофантовых уравнений, в частности уравнения Туэ и уравнений, задающих кривые рода 1, а также дать еще одно решение проблемы десятого дискриминанта, установить границу для дискриминантов двухклассных мнимых квадратичных полей, оценить снизу наибольший простой делитель значений бинарной формы степени >3 и величину свободного от квадратов ядра целочисленного многочлена (см. [2]).

Лит.:[1] Спринджук В. Г., "Изв. АН СССР. Сер. матем.", 1971, т. 35, № 5, с. 991 - 1007; 1972, т. 36, № 4, с. 712- 741; [2] его же, в сб.: Актуальные проблемы аналитической теории чисел, Минск, 1974, с. 178-98; [3] Фельдман Н. И., там же, с. 244-68; [4] е г о же, "Изв. АН СССР. Сер. матем.", 1971, т. 35, №5, с. 973-90; [5] Baker A., "Phil. Trans. Royal Soc. London", Ser. A., 1968, v. 263, p. 173-91, 193-208; [6] его же, в кн.: Actes du Congrfs International des Mathematiciens. 1970, t. 1, P., 1971, p. 19-26.

В. Г. Спринджук.