- ДИНАМИКА СОРБЦИИ
- процесс поглощения адсорбата (паров, газов или растворенного вещества) твердым телом, сопровождающийся адсорбцией и абсорбцией, т. е. соответственно поверхностным и объемным поглощением. Д. с. определяется скоростями адсорбции, внешней и внутренней диффузией адсорбата, и описывается системой дифференциальных уравнений диффузионного переноса вещества с учетом кинетики адсорбции. В большинстве случаев процесс сорбции происходит в неизотермических условиях - при выделении теплоты адсорбции и при капиллярной конденсации -так что процессы переноса массы вещества (диффузия) сопровождаются переносом тепла (теплообменом), т. е. описываются системой дифференциальных уравнений массо- и теплопереноса. Если адсорбентом является смесь газов и паров или смесь растворенных веществ, то молекулярный перенос массы вещества и тепла описывается системой уравнений Онсагера (см. |2]).
В случае бинарной смеси система дифференциальных уравнений тепло- и массопереноса, решение к-рой, при соответствующих краевых условиях, определяет Д. с, имеет вид
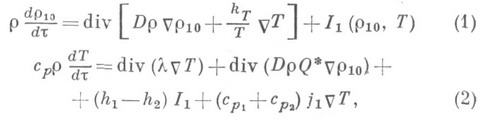
где r10 - относительная плотность компоненты "1", r10=r1/p; r=r1+r2, D- коэффициент диффузии, Т- температура, т - время, с р- удельная изобарная теплоемкость, X- коэффициент теплопроводности, Q*- изотермич. теплота переноса, kT- термодиффузионная постоянная, h- удельная энтальпия, j1- диффузионный поток массы компоненты "1", d/dt- полная или субстанциональная производная, равная

(где v- скорость движения центра тяжести потока адсорбата), I1(r10, T)- мощность источника массы вещества, обусловленная кинетикой адсорбции и фазовыми превращениями, к-рые в общем случае являются функциями концентрации r10 и температуры Т.
Скорость vдвижения потока адсорбата получается из решений Навье- Стокса уравнений. Краевые условия определяются характером и физич. механизмом взаимодействия поверхности твердого тела с окружающей средой (адсорбатом). При этом скорость массообмена определяется внешней диффузией адсорбата к поверхности тела и кинетикой адсорбции. Обычно рассматривают два крайних случая:
1) массообмен определяется диффузией;
2) концентрация на поверхности тела зависит только от скорости адсорбции.
Для случая сорбции пара капиллярнопористыми телами получены решения системы дифференциальных уравнений (1), (2) применительно к телам простейшей формы (см. [1]).
Процесс десорбции водяного пара пористыми телами составляет часть процесса сушки. Д. с. в этом случае рассчитывается приближенно по следующим уравнениям массо- и теплообмена

где
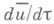 - скорость десорбции, r - удельная теплота сорбции, r0 - плотность сухого тела, q(t)- удельный поток тепла на поверхности тела, Rv- гидравлич. радиус тела,
- скорость десорбции, r - удельная теплота сорбции, r0 - плотность сухого тела, q(t)- удельный поток тепла на поверхности тела, Rv- гидравлич. радиус тела,  - среднее влагосодержание (относительная концентрация) тела,
- среднее влагосодержание (относительная концентрация) тела,  - равновесное влагосодержание, х - относительный коэффициент сушки, N- скорость сушки в первом периоде - периоде постоянной скорости, Rb - число Ребиндера.
- равновесное влагосодержание, х - относительный коэффициент сушки, N- скорость сушки в первом периоде - периоде постоянной скорости, Rb - число Ребиндера.Лит.:[1] Лыков А. В., Михайлов Ю. А., Теория тепло- и массопереноса, М.-Л., 1963; [2] Де Гроот С, Мазур П., Неравновесная термодинамика, пер. с англ., М., 1964; [3] Лыков А. В., Теория сушки, 2 изд., М., 1968; [4] Франк-Каменецкий Д. А., Диффузия и теплопередача в химической кинематике, 2 изд., М., 1967; [5] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М., 1966.
А. В. Лыков.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
