ДИНАМИКА

- раздел механики, в к-ром изучается движение материальных тел, происходящее под действием приложенных к ним сил, вызывающих или изменяющих это движение,- так называемых ускоряющих сил.

Основы Д. заложены в нач. 17 в. Г. Галилеем (G. Galilei), к-рый первый рассмотрел движение тел под действием силы тяжести и установил закон инерции. Основные принципы Д. были четко сформулированы И. Ньютоном (I. Newton) в виде трех основных законов механики и следствий из них. Дальнейшее развитие и совершенствование законов Д. содержится в трудах Л. Эйлера (L. Euler), Ж. Д'Аламбера (J. D'Alembert), Ж. Лагранжа (J. Lagrange), где были даны общие методы составления уравнений Д. Начало аналитич. методам исследования уравнений Д. положили Ж. Лагранж, У. Гамильтон {W. Hamilton) и К. Якоби (С. Jacobi). Позднейшим развитием этих методов занимались К. Гаусс (С. Gauss), M. В. Остроградский, А. Пуанкаре (Н. Poincare), С. А. Чаплыгин, Н. Г. Четаев и др.

Д., основывающаяся на принципах Г. Галилея и И. Ньютона, наз. классической или ньютоновской Д., в отличие от направлений, исходящих из иных принципов (квантовая механика, релятивистская Д. и др.). Классич. Д. состоит из совокупности математич. выводов и заключений, являющихся следствиями основных законов Галилея и Ньютона. В ней аксиоматически вводятся понятия неподвижного пространства (абсолютной неподвижной системы отсчета или инерциальной системы отсчета) и абсолютного времени, одинакового для всех точек пространства. Абсолютному пространству приписываются геометрич. свойства евклидова пространства. Законы Ньютона формулируются по отношению к абсолютному пространству и абсолютному времени. Они остаются справедливыми по отношению к инерциальным системам отсчета. Заключения о движении материальных тел Д. получает с помощью построения моделей (материальной точки, абсолютно твердого тела, континуума и др.).

По характеру решаемых задач Д. может быть разделена на Д. материальной точки и Д. системы материальных точек. Понятие материальной точки является основным понятием классической Д. Материальной точкой наз. такое тело, геометрич. размерами к-рого можно пренебрегать при изучении его движения, но к-рое обладает конечной массой. Первый и второй законы Ньютона формулируются в Д. только для одной материальной точки. Кроме материальной точки в Д. рассматривают еще модель абсолютно твердого тела, расстояния между точками к-рого не изменяются во время движения. Эти основные модели Д. позволяют успешно решать ряд конкретных задач о движении реальных тел.

В Д. системы материальных точек рассматриваются движения таких тел, к-рые находятся во взаимосвязи друг с другом. Д. системы включает в себя Д. твердого тела, Д. систем с переменной массой, Д. упругого и пластически деформируемого тела, Д. жидкости и газа и др.

Характер движения материальной системы определяется действующими на нее силами (активными силами), а также связями, наложенными на точки системы, действие к-рых может быть заменено действием сил реакций связи (пассивными силами). Действующие на систему материальных точек силы являются результатом взаимодействия отдельных материальных точек, как входящих, так и не входящих в рассматриваемую систему. В соответствии с этим различают силы внутренние и внешние. Силы могут быть представлены как функции положений материальных точек, их скоростей и времени.

В Д. решаются две основные задачи: 1) определение силы, производящей данное движение материальной точки или системы; 2) определение движения материальной точки или системы, происходящее под действием заданных сил. Задачи Д. решаются при помощи дифференциальных уравнений движения. Для одной материальной точки эти уравнения выражают второй закон Ньютона и могут быть записаны в виде

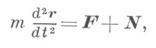
где r- радиус-вектор материальной точки в рассматриваемой системе отсчета, d²r/dt²- ее ускорение, F- действующая на точку активная сила, N- сила реакций связи. Для определения закона движения материальной точки нужно найти значение rдля каждого момента времени. Задача интегрирования уравнений Д. решается с помощью общих теорем Д. (теорем об изменении количества движения, момента количества движения и живых сил). Эти теоремы обусловливают важные физич. зависимости между основными динамич. характеристиками движения и взаимодействия материальных тел; в ряде случаев они значительно упрощают процесс интегрирования уравнений Д. Кроме того, общие теоремы дают возможность изучать отдельные стороны рассматриваемого движения. Общие теоремы для системы материальных точек могут быть получены непосредственным обобщением общих теорем для одной материальной точки. При выводе из Д'Аламбера- Лагранжа принципа они становятся более совершенными и не содержат реакций связи, а устанавливают непосредственную зависимость между динамич. величинами, характеризующими движение системы, и действующими на систему активными силами. Наиболее распространенными являются системы с голономными идеальными связями. Движение таких систем полностью описывается Лагранжа уравнениями2-го рода, получающимися из принципа Д'Аламбера - Лагранжа. Эти уравнения наиболее удобны при исследовании движения системы материальных точек. Для материальных систем с неголономными идеальными связями наиболее общими уравнениями движения, не содержащими реакций связей, являются Аппеля уравнения.

Изучением свойств уравнений движения механич. систем, обусловленных специфич. формой этих уравнений, занимается аналитич. Д. Она рассматривает общие принципы Д., вывод из этих принципов дифференциальных уравнений движения и методов их интегрирования. Методы аналитич. Д. широко применяются как для решения различных задач Д., так и в различных областях физики. Большое значение для исследования свойств движения механич. систем получили канонические Гамильтона уравнения, к-рые дают возможность сформулировать ряд эффективных методов решения задач Д.

Помимо установления общих методов составления и интегрирования уравнений движения материальных тел, движущихся под действием ускоряющих сил, в Д. рассматривается ряд специальных задач: Д. твердого тела, Д. гироскопич. систем, теория колебаний механич. систем, теория устойчивости движения, теория удара и др.

Лит.:[1] Галилей Г., Соч., т. 1 - Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению..., пер. с итал., М.-Л., 1934; [2] его же, Диалог о двух главнейших системах мира, птолемеевой и коперниковой, пер. с итал., М.-Л., 1948; [3] Ньютон И., Математические начала натуральной философии, пер. с латин., в кн.: Крылов А. Н., Собр. трудов, т. 7, М.-Л., 1936; [4] Эйлер Л., Основы динамики точки, пер. с латин., М.-Л., 1938; [5] Д' Аламбер Ж., Динамика, пер. с франц., М.-Л., 1950; [6] Лагранж Ж., Аналитическая механика, пер. с франц., т. 1-2, М.-Л., 1950; [7] Якоби К., Лекции по динамике, пер. с нем.,М.-Л., 1936; [8] Гамильтон У., Об общем методе в динамике ..., пер. с англ., в кн.: Вариационные принципы механики, М., 1959; [9] Герц Г., Принципы механики, изложенные в новой связи, пер. с нем., М., 1959; [10] Остроградский М. В., Лекции по аналитической механике, в кн.: Остроградский М. В., Поли. собр. трудов, т. 2, К., 1961; [11] Жуковский Н. Е., Теоретическая механика, 2изд., М.-Л., 1952; [12] Чаплыгин С. А., Курсы лекций по теоретической механике, Собр. соч., т. 4, М,-Л., 1949; [13] Четаев Н. Г., Устойчивость движения.-Работы по аналитической механике, М., 1962.

Е. Н. Березкин.