ДИАГРАММА

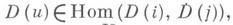в категории С- отображение Dориентированного графа Г с множеством вершин I и с множеством дуг Uв категорию С, при котором причем если дуга имеет начало iи конец j. Иногда под диаграммой в Спонимается образ отображения D, что позволяет использовать наглядное изображение диаграммы.

Пусть j=(u₁, . . . , и _п)- ориентированная цепь графа Г с началом iи концом j, т. е. непустая конечная последовательность дуг, в к-рой началом каждой дуги служит конец предыдущей; и пусть D(j): означает композицию морфизмов:

Диаграмма Dназывается коммутативной, если D(j)=Z) (j') всякий раз, как j и j', являются ориентированными цепями с одним и тем же началом и концом.

Наиболее часто встречаемые виды Д.- это последовательности, треугольные диаграммы и квадратные диаграммы. Для определения последовательности за определяющий граф берется граф вида

Соответствующая Д. изображается следующим образом:

здесь A_k=D(i_k)- объекты категории С,a f_k=D(u_k)- морфизмы этой категории.

Треугольная Д. в категории Ссоответствует графу и изображается:

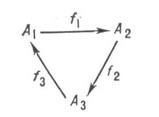
Коммутативность этой Д. означает, что

Квадратная Д. соответствует графу и изображается:

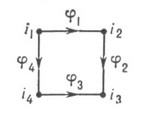
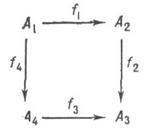
Коммутативность этой Д. означает, что

Класс Д. с одним и тем же графом Г образует категорию. За морфизм диаграммы Dв диаграмму D' принимается семейство морфизмов v_i : где iпробегает множество вершин графа Г, что для любой дуги ис началом iи концом j выполняется условие =. В частности, можно говорить об изоморфных Д. Любую категорию можно представить как категорию диаграмм с нек-рым графом. Иногда граф Г наз. схемой диаграмм в С.

Лит.:[1] Гротендик А., О некоторых вопросах гомологической алгебры, пер. с франц., М., 1961.

И. В. Долгачев.