ДВУХ ТЕЛ ЗАДАЧА

- задача о движении в трехмерном евклидовом пространстве Е ³ двух материальных точек Р ₁ и Р ₂ с массами т ₁ и т ₂ под действием ньютонова притяжения. Д. т. з. является частным случаем задачи птел, к-рая описывается системой обыкновенных дифференциальных уравнений порядка вп и имеет 10 независимых интегралов: 6 - движения центра инерции, 3 - площадей и 1 - энергии (см. [1]). Д. т. з. имеет, кроме того, еще три интеграла Лапласа (из них один независим от предыдущих) и является полностью интегрируемой (см. [2]).

Интегрирование Д. т. з. удобнее производить в специальных системах координат, использующих указанные интегралы. Если начало декартовых координат х, y, z поместить в точку Р ₁ (при этом используются все 6 интегралов движения центра инерции) и ось zнаправить по вектору, составленному из интегралов площадей (при этом используются два интеграла площадей), то движение точки Р ₂ происходит в плоскости z=0и удовлетворяет системе

(1)

где m=f(m₁+m₂), f - гравитационная

постоянная. Система (1) имеет 4 интеграла:

су- mxr^-1 = l₁ и cx+myr^-1 =-l₂ (Лапласа), связанных соотношением

При этом

(2)

т. е. орбиты точки Р ₂ суть конич. сечения с параметром р=с²/m, большой полуосью a=-m/(2h), эксцентриситетом долготой перицентра со

и с фокусом в начале координат. Положение точки Р ₂ на орбите определяют истинной аномалией v, отсчитываемой от направления на перицентр; тогда (2) дает r=p/(1+ecos v). Если , то возможны три типа орбит (I) при h<0 это - эллипсы, тогда

(II) при h>0 это - гиперболы, тогда

(III) при h=0 это - параболы, тогда

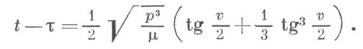
Здесь t - момент прохождения через перицентр, и- эксцентрическая аномалия. Если c=0, то движение происходит по прямой линии. Д. т. з. описывает невозмущенное кеплерово движение планеты относительно Солнца либо спутника относительно планеты и т. п. Лит.:[1] Зигель К. Л., Лекции по небесной механине, пер. с нем., М., 1959; [2] Абалакия В. К. (и др.), Справочник по небесной механике и астродинамике, М., 1971.

А. Д. Брюно.