ТРЕХ ТЕЛ ЗАДАЧА

- задача о движении трех тел, рассматриваемых как материальные точки, взаимно притягивающихся по закону тяготения Ньютона. Классич. пример Т. т. з.- задача о движении системы Солнце - Земля - Луна. Т. т. а. состоит в нахождении общего решения системы дифференциальных уравнений вида

где x_i, y_i, z_i - прямоугольные координаты тела M_i в нек-рой абсолютной системе координат с неизменными направлениями осей, t - время, m_i - масса тела М _i,a U - силовая функция, зависящая только от взаимных расстояний между телами. Функция Uопределяется соотношением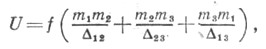

где взаимные расстояния i, j=1, 2, 3, даются формулой

Из свойств силовой функции выводятся десять первых интегралов уравнений движения в абсолютной системе координат. Шесть из них, называемые интегралами движения центра масс, определяют равномерное и прямолинейное движение центра масс трех тел. Три интеграла моментов количества движения задают неизменную величину и направление вектора момента количества движения системы трех тел. Интеграл энергии определяет постоянную величину полной энергии системы. Г. Брунс (Н. Bruns, 1887) доказал, что уравнения движения Т. т. з. не имеют никаких других первых интегралов, выражающихся с помощью алгебраич. функций от координат и их производных. А. Пуанкаре (Н. Poincare, 1889) доказал, что уравнения движения Т. т. з. не имеют также трансцендентных интегралов, выражающихся через однозначные аналитич. ции. К. Сундман (С. Sundman, 1912) нашел общее решение задачи в виде степенных рядов относительно нек-рой регуляризирующей переменной, сходящихся для любого момента. Однако ряды Сундмана оказались совершенно бесполезными как для качественных исследований, так и для практических вычислений вследствие их крайне медленной сходимости.
Уравнения Т. т. з. допускают пять частных решении, в к-рых все три материальные точки находятся в некоторой неизменной плоскости. При этом конфигурация трех тел остается неизменной, и они описывают кеплеровские траектории с общим фокусом в центре масс системы. Два частных решения соответствуют случаю, когда три тела все время образуют равносторонний треугольник. Это - т. н. треугольные решения Т. т. з., или р ешения Лагранжа. Три частных решения, соответствующие расположению всех трех тел на одной прямой, наз. прямолинейными частными решениями Т. т. з., или решениями Эйлера.
Для общего случая Т. т. з. подробно изучены финалъные движения, т. е. предельные свойства движения при и
Частным случаем Т. т. з. является т. <н. ограниченная Т. т. з., к-рая получается из общей Т. т. з. в том случае, когда масса одного из трех тел столь мала, что ее влиянием на движение остальных двух тел можно пренебречь. В этой задаче тела М ₁ и М ₂ с конечными массами т ₁ и m₂ движутся под действием сил взаимного притяжения по кеплеровским орбитам. В правой прямоугольной системе координат с началом Gвцентре масс тел М ₁ и М ₂, с осью 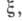направленной по линии, соединяющей тела М ₁ и М ₂, и осью перпендикулярной плоскости их движения, движение третьего тела М ₃ с малой массой описывается следующими дифференциальными уравнениями: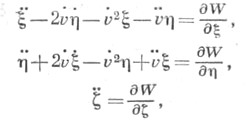

где

v - истинная аномалия кеплеровского движения тел М ₁ и М ₂, а r₁ и r₂- расстояния от тела М ₃ до тел М ₁ и М ₂ соответственно. В случае круговой ограниченной Т. т. з. и уравнения движения тела М ₃ имеют первый интеграл, наз. интегралом Якоби, вида

где С - произвольная постоянная. Поверхность, определяемая уравнением

наз. поверхностью нулевой скорости и замечательна тем, что определяет области возможных движений тела М ₃ относительно тел М ₁ и М ₂. Ограниченная Т. т. з. имеет частные решения, аналогичные частным решениям общей Т. т. з. Положения тела с малой массой при этих частных решениях наз. точками либрации.
Для ограниченной задачи удалось исследовать разнообразные классы периодич. движений.

Лит.:[1] Дубошин Г. Н., Небесная механика. Аналитические и качественные методы, 2 изд., М., 1978; [2] Субботин М. Ф., Введение в теоретическую астрономию, М., 1968.
Е. П. Аксенов.