ДВОЙСТВЕННОСТИ ПРИНЦИП

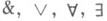- 1) Д. п. в математической логике - теорема о взаимозаменяемости в определенном смысле логич. операций в формулах формальных логических и логико-предметных языков. Пусть А- формула языка логики высказываний или логики предикатов, не содержащая знака импликации ; формула А* наз. двойственной формуле А, если она может быть получена из Азаменой в Акаждого вхождения символов двойственными им операциями, т. е. соответственно символами Д. п. гласит, что если 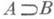истинно, то истинно В частности, если формулы А и В эквивалентны, то эквивалентны и двойственные им формулы А* и В*. Д. п. справедлив для классич. систем, при этом эквивалентность и истинность формул в его формулировке могут пониматься как в терминах интерпретаций, так и в смысле выводимости в соответствующем классич. исчислении. При конструктивном понимании формул Д. п. перестает действовать. Так, напр., в языке логики высказываний импликация конструктивно верна и даже выводима в Гейтинга формальной системе, однако обратная импликация двойственных формул конструктивно неверна (напр., нереализуема по Клини - Роузу).

С Д. п. тесно связана следующая теорема: если F*( А ₁,..., А _n) - формула, двойственная пропозициональной или предикатной формуле F(A₁,. . ., А _п), построенной без употребления импликации из элементарных высказываний А ₁,. . ., А _п, то формула F(A₁,..., А _п )эквивалентна формуле в классич. исчислении высказываний или предикатов, соответственно.

Лит.:[1] Новиков П. С, Элементы математической логики, М., 1959; [2] К лини С. К., Введение в метаматематику, пер. с англ., М., 1957.

Ф. А. Кабаков.

2) Д. п. в геометрии - принцип, формулируемый в нек-рых разделах геометрии и заключающийся в том, что, заменяя в любом верном предложении все

I входящие в него понятия на двойственные им, получают верное (двойственное первому) предложение. Справедливость Д. п. в проективной геометрии вытекает из того, что каждой аксиоме проективной геометрии соответствует двойственное предложение, являющееся либо аксиомой, либо теоремой.

В проективной геометрии на плоскости двойственными являются понятия:

точка	прямая
точка, инцидентная прямой алгебраическая пиния порядка пкасательная прямая к линии	прямая, инцидентная точке алгебраический пучок прямых класса пхарактеристическая точка пучка

Если считать отношением инцидентности между точкой и линией второго порядка принадлежность точки линии второго порядка, а отношением инцидентности прямой с линией второго порядка - касание прямой к линии второго порядка, то понятием, двойственным линии второго порядка, является линия второго порядка. Примером пары двойственных утверждений могут служить Брианшона теорема и Паскаля теорема. В проективной геометрии в пространстве двойственны понятия точки и плоскости; понятие прямой само себе двойственно.

Д. п. имеет место и в эллиптич. геометрии, где, кроме понятий проективной геометрии двойственными являются понятия отрезка и угла. Так. напр., в эллиптич. геометрии справедливы следующие два двойственных утверждения:

два треугольника равны, если три стороны одного соответственно равны трем сторонам другого

два треугольника равны, если три угла одного соответственно равны трем углам другого

Лит.:[1] Ефимов Н. В., Высшая геометрия, 5 изд., М., 1971.

А. С, Пархоменко.

3) Д. п. в проективной геометрии состоит в том, что любой теореме относительно подпространств S_a, S_b, . . . проективного пространства ПД их пересечений и сумм соответствует теорема относительно подпространств S_n_ _а_₁ S_n-b-1,... их сумм и пересечений. Д. п. определяется двойственным характером аксиом проективной геометрии и вытекающих из них теорем. Для проективного пространства П _n (Х)над телом КД. п. справедлив тогда и только тогда, когда Кдопускает инверсный автоморфизм. В общем случае имеет место двойственность между проективными пространствами П _п (Х). и П _п( К*), тела Ки K* к-рых инверсно изоморфны: таковы, напр., левое и правое проективные пространства Р _п^l (К). и Р _п^r (К)над К(см. Проективная алгебра, Корреляция), причем соответствие между ними, т. е. соответствие между S_k и S_n-k-1 определяется выбором пары координатных систем в П _п (К). и П _n( К*). Д. п. можно обосновать также с помощью дуальных отображений линейных пространств q _п+1 (К). над телом, к-рые используются для интерпретации проективных пространств.

М. И. Вопцеховский.

4) Д. <п. в частично упорядоченных множествах: если верна какая-либо теорема о частично упорядоченных множествах, сформулированная в общелогич. терминах и терминах порядка, то верна и двойственная ей теорема. Для получения теоремы, двойственной к данной, все высказывания и понятия, относящиеся к порядку, заменяются на двойственные (т. е. все знаки порядка < заменяются на >, и обратно), а общелогич. термины остаются без изменений. Из справедливости нек-рого утверждения для конкретного частично упорядоченного множества (или для конкретного класса частично упорядоченных множеств) еще не вытекает справедливость двойственного утверждения для этого множества. Так, частично упорядоченное множество может иметь наименьший элемент, но не иметь наибольшего, оно может удовлетворять условию минимальности, но не удовлетворять условию максимальности. Справедливость Д. п. вытекает из того, что отношение, обратное к частичному порядку, само является частичным порядком. Иногда под Д. п. понимают именно это утверждение.

Т. С. Фофанова.