ГУРВИЦА ТЕОРЕМА

ГУРВИЦА ТЕОРЕМА

если 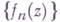- последовательность голоморфных функций в области , равномерно сходящаяся внутри Dк функции , то для любой замкнутой спрямляемой жордановой кривой Г, лежащей в Dвместе с областью, ограниченной Г, и не проходящей через нули функции f(z), можно указать такое число 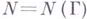, что при каждая из функций 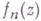имеет внутри Г одно и то же число нулей, равное числу нулей функции 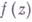внутри Г. Получена А. Гурвицем [1].

Лит.: [1] Hurwitz A., "Math. Ann.", 1895, Bd 46, S. 273-84; то же: Math. Werke, Bd 2, Basel, 1933, S. 533-45; [2] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967. Е. Д. Соломенцев.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужно сделать НИР?

Смотреть что такое "ГУРВИЦА ТЕОРЕМА" в других словарях:

  • Теорема Рауса — Гурвица — Теорема Рауса  Гурвица предоставляет возможность определить, является ли данный многочлен устойчивым по Гурвицу. Была доказана в 1895 году и названа в честь Эдварда Джона Рауса (англ.) и Адольфа Гурвица. Содержание 1 Условные… …   Википедия

  • Теорема Рауса — Теорема Рауса  Гурвица предоставляет возможность определить, является ли данный многочлен устойчивым по Гурвицу. Была доказана в 1895 году и названа в честь Эдварда Джона Рауса (англ.) и Адольфа Гурвица. Содержание 1 Условные… …   Википедия

  • Гурвица критерий — Критерий устойчивости Гурвица один из способов анализа линейной стационарной динамической системы на устойчивость, разработанный немецким математиком Адольфом Гурвицем. Наряду с критерием Рауса является представителем семейства алгебраических… …   Википедия

  • Теорема Кэли о числе деревьев — У этого термина существуют и другие значения, см. Теорема Кэли. Полный список деревьев на 2, 3 и 4 пронумерованных вершинах …   Википедия

  • РАУСА ТЕОРЕМА — теорема, позволяющая для многочлена f(х)с действительными коэффициентами (в регулярном случае) определить с помощью схемы Рауса число комплексных корней этого многочлена с положительной действительной частью. Пусть многочлен f (х)для удобства… …   Математическая энциклопедия

  • ЧАСТОТНАЯ ТЕОРЕМА — теорема, формулирующая условия разрешимости уравнений Лурье где заданные матрицы размеров соответственно, Н=Н*, h искомые матрицы размера nX . и . Х т. Уравнения Лурье имеют две другие эквивалентные формы: при где и в общем случае где заданная… …   Математическая энциклопедия

  • Теорема Рауса—Гурвица — …   Википедия

  • Теорема Рута-Гурвица — …   Википедия

  • Критерий устойчивости Гурвица — Критерий устойчивости Рауса Гурвица один из способов анализа линейной стационарной динамической системы на устойчивость, разработанный немецким математиком Адольфом Гурвицом. Наряду с критерием Рауса является представителем семейства… …   Википедия

  • Критерий Гурвица — Критерий устойчивости Гурвица один из способов анализа линейной стационарной динамической системы на устойчивость, разработанный немецким математиком Адольфом Гурвицем. Наряду с критерием Рауса является представителем семейства алгебраических… …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»