- ГРАММАТИКА СОСТАВЛЯЮЩИХ
грамматика непосредственно составляющих, НС-грамматика, грамматика контекстная,- частный случай грамматики порождающей,
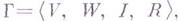 когда каждое ее правило имеет вид
когда каждое ее правило имеет вид  , где
, где 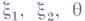 - цепочки в алфавите
- цепочки в алфавите  и 0 непуста. Каждый шаг вывода в Г. с. состоит в замене одного вхождения символа Авхождением цепочки q, причем возможность замены обусловлена наличием "контекста"
и 0 непуста. Каждый шаг вывода в Г. с. состоит в замене одного вхождения символа Авхождением цепочки q, причем возможность замены обусловлена наличием "контекста"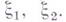
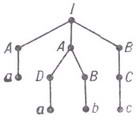
Вхождения символов в q потом также могут заменяться и т. д. Таким образом, вхождение символа "развертывается" в нек-рый отрезок возникающей в результате вывода цепочки. Это дает возможность представить вывод в Г. с. с помощью дерева (дерева вывода):
напр., если грамматика имеет правила
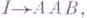
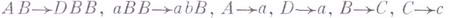 (
( - основные символы,
- основные символы,  - вспомогательные символы, I - начальный символ), то вывод
- вспомогательные символы, I - начальный символ), то вывод 
 имеет дерево, изображенное на рис. Множество всех отрезков последней цепочки вывода, получающихся "развертыванием" вхождений вспомогательных символов - иначе говоря, "происходящих" от (неконцевых) вершин дерева вывода - при добавлении всех одноточечных отрезков образует систему составляющих указанной цепочки (см. Синтаксическая структура);отсюда и название "Г. с.". Если все одноточечные отрезки также получаются заменой вхождений вспомогательных символов, то можно получить размеченную систему составляющих, приписывая каждой составляющей в качестве меток те вспомогательные символы, от вхождений к-рых она "происходит"; так, в приведенном выше примере для цепочки
имеет дерево, изображенное на рис. Множество всех отрезков последней цепочки вывода, получающихся "развертыванием" вхождений вспомогательных символов - иначе говоря, "происходящих" от (неконцевых) вершин дерева вывода - при добавлении всех одноточечных отрезков образует систему составляющих указанной цепочки (см. Синтаксическая структура);отсюда и название "Г. с.". Если все одноточечные отрезки также получаются заменой вхождений вспомогательных символов, то можно получить размеченную систему составляющих, приписывая каждой составляющей в качестве меток те вспомогательные символы, от вхождений к-рых она "происходит"; так, в приведенном выше примере для цепочки 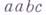 получается размеченная система составляющих
получается размеченная система составляющих

(здесь границы составляющих указаны скобками, после правых скобок записаны метки). Приписывание цепочкам размеченных систем составляющих лежит в основе лингвистич. приложений Г. с. Так, грамматика, имеющая (в числе прочих) правила

где ПРЕДЛ,
 - вспомогательные символы, означающие, соответственно, "предложение", "существительное рода хв числе уи падеже г", "группа глагола в 3-м лице", "переходный глагол в 3-м лице", а символ ПРЕДЛ - начальный, приписывает предложению "Эллипс пересекает параболу" размеченную систему составляющих
- вспомогательные символы, означающие, соответственно, "предложение", "существительное рода хв числе уи падеже г", "группа глагола в 3-м лице", "переходный глагол в 3-м лице", а символ ПРЕДЛ - начальный, приписывает предложению "Эллипс пересекает параболу" размеченную систему составляющих
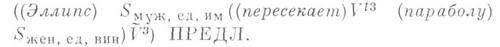
Математич. значение Г. с. определяется прежде всего тем, что порождаемые ими языки (так наз. НС-языки) представляют собой простой подкласс класса примитивно рекурсивных множеств: класс НС-языков совпадает с классом языков, допускаемых недетерминированными линейно ограниченными Тьюринга машинами с одной лентой п одной головкой. "Конкретные" числовые множества при обычных способах кодирования натуральных чисел весьма часто оказываются НС-языками (таковы, напр., множество полных квадратов, множество простых чисел, множество десятичных приближений числа
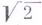 и т. п.).
и т. п.).
Для каждой Г. с. может быть построена эквивалентная ей левоконтекстная (соответственно правоконтекстная) Г. с., то есть Г. с., все правила к-рой имеют вид
 (соответственно
(соответственно 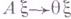 ). В то же время всякая Г. с., все правила к-рой имеют вид
). В то же время всякая Г. с., все правила к-рой имеют вид 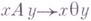 , где х, у - цепочки в основном алфавите, эквивалентна нек-рой грамматике бесконтекстной.
, где х, у - цепочки в основном алфавите, эквивалентна нек-рой грамматике бесконтекстной.
Класс НС-языков замкнут относительно объединения, пересечения, умножения, усеченной итерации, подстановки; неизвестно, замкнут ли он относительно дополнения.
Сложность вывода. Временная сложность вывода в Г. с. ограничена сверху показательной функцией. Существуют языки, порождаемые Г. с. с временной сложностью порядка
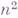 и не порождаемые никакими Г. с. с меньшей по порядку временной сложностью (например, язык
и не порождаемые никакими Г. с. с меньшей по порядку временной сложностью (например, язык 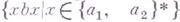 ); примеров более высоких нижних оценок временной сложности неизвестно. Емкость всякой Г. с. очевидным образом равна п;для произвольной порождающей грамматики, емкость к-рой ограничена сверху линейной функцией
); примеров более высоких нижних оценок временной сложности неизвестно. Емкость всякой Г. с. очевидным образом равна п;для произвольной порождающей грамматики, емкость к-рой ограничена сверху линейной функцией
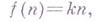
существует эквивалентная ей Г. с. (эта Г. с. может быть построена эффективно, если известно k).
Алгоритмические проблемы. Если нек-рый класс языков содержит хотя бы один НС-язык н хотя бы для одного
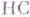 -языка
-языка 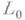 содержит разве лишь конечное число "почти совпадающих" с
содержит разве лишь конечное число "почти совпадающих" с 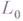 языков (языки
языков (языки 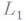 и
и  "почти совпадают", если их симметрия, разность
"почти совпадают", если их симметрия, разность 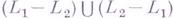 конечна), то свойство принадлежать данному классу нераспознаваемо в классе Г. с.
конечна), то свойство принадлежать данному классу нераспознаваемо в классе Г. с.
В частности, нераспознаваемы свойства быть пустым, конечным, автоматным, линейным, бесконтекстным языком, иметь пустое или конечное дополнение, совпадать с (любым) фиксированным
 -языком. Примером свойства языков, распознаваемого в классе Г. с., может служить свойство содержать (любую) фиксированную цепочку.
-языком. Примером свойства языков, распознаваемого в классе Г. с., может служить свойство содержать (любую) фиксированную цепочку.
См. также Грамматика бесконтекстная.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
