- ГОМОМОРФИЗМ
- морфизм в категории алгебраических систем. Г.- отображение алгебраич. системы
, сохраняющее основные операции и основные отношения; точнее, пусть 
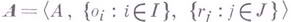- алгебраич. система с основными операциями 
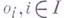и основными отношениями 
, 
Г. системы 
в однотипную ей систему 
наз. отображение 
, удовлетворяющее следующим двум условиям:
для всех элементов
из Аи всех 
Если каждому элементу iиз I сопоставлен некоторый
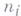-арный функциональный символ 
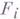, а каждому элементу j из 
- mj -местный предикатный символ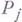 
и в каждой системе 
, однотипной системе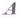 
, результат i-й основной операции 
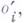примененной к элементам 
из 
, записан в виде 
, а вместо 
пишут 
. Условия (1), (2) при этом упрощаются и принимают вид
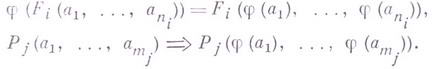
Г. ф :
наз. сильным, если для любых элементов 
из 
и для любого предикатного символа 
условие 
влечет существование в Атаких элементов 
что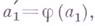 
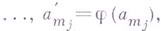и выполняется соотношение 
. Для алгебр понятия Г. и сильного Г. совпадают. Для моделей существуют Г., к-рые не являются сильными, и взаимно однозначные Г., к-рые не являются изоморфизмами.
Если
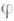- Г. алгебраич. системы 
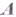на алгебраич. систему 
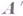и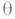 
- ядерная конгруэнция для Г. 
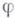, то отображение 
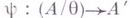, определяемое формулой 
, является Г. факторсистемы 
на алгебраич. систему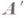 
. Если при этом 
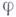- сильный Г., то 
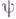есть изоморфизм. Это - одна из самых общих формулировок теоремы о Г.
Следует отметить, что иногда Г. наз. также морфизмы в категориях, отличных от категорий алгебраич. систем. (Напр., Г. графов, Г. пучков, Г. групп Ли).
Лит.:[1] Мальцев А. И., Алгебраические системы, М., 1970; [2] С hang С. С., Keisler H. J., Model theory, Amsterdam, 1973. Д. М. Смирнов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
