- ГОМЕОМОРФИЗМ
- взаимно однозначное соответствие между двумя топологич. пространствами, при к-ром оба взаимно обратных отображения, определяемые этим соответствием, непрерывны. Эти отображения наз. гомеоморфными, или топологическими, отображениями, а также гомеоморфизмами, а о пространствах говорят, что они принадлежат одному топологическому типун наз. гомеоморфными, или топологически эквивалентными. Они являются изоморфными объектами в категории топологич. пространств и непрерывных отображений. Следует отличать Г. от уплотнения (в к-ром непрерывность обязательна только в одну сторону); однако уплотнение бикомпакта на хаусдорфово пространство является Г.
Примеры. 1) Функция
 устанавливает Г. между числовой прямой
устанавливает Г. между числовой прямой 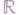 и интервалом
и интервалом 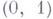 ; 2) замкнутый круг гомеоморфен любому замкнутому выпуклому многоугольнику; 3) трехмерное проективное пространство гомеоморфно группе вращений пространства R3 вокруг начала и также пространству единичных касательных векторов к сфере
; 2) замкнутый круг гомеоморфен любому замкнутому выпуклому многоугольнику; 3) трехмерное проективное пространство гомеоморфно группе вращений пространства R3 вокруг начала и также пространству единичных касательных векторов к сфере 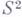 ; 4) все бикомпактные нульмерные группы со счетной базой гомеоморфны канторову множеству; 5) бесконечномерные и сепарабельные банаховы пространства и даже пространства Фреше гомеоморфны между собой; 6) сфера и тор негомеоморфны.
; 4) все бикомпактные нульмерные группы со счетной базой гомеоморфны канторову множеству; 5) бесконечномерные и сепарабельные банаховы пространства и даже пространства Фреше гомеоморфны между собой; 6) сфера и тор негомеоморфны.
Термин "Г." был введен А. Пуанкаре (Н. Poincare) в 1895 (см. [3]) в применении к (кусочно) дифференцируемым отображениям областей и подмногообразий пространства
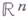 ; однако понятие было известно и ранее, напр. Ф. Клейну (F. Klein; 1872) и в рудиментарной форме А. Мёбиусу (А.
; однако понятие было известно и ранее, напр. Ф. Клейну (F. Klein; 1872) и в рудиментарной форме А. Мёбиусу (А.  - элементарное сродство, 1863). В начале 20 в. под влиянием развития теории множеств и аксиоматич. метода началось изучение Г. без предположений дифференцируемости. Такая задача, в явной форме впервые поставленная Д. Гильбертом (D. Hilbert) (см. [7], с. 31), составляет содержание пятой проблемы Гильберта. Особое значение имело установление Л. Брауэром (L. Brouwer) негомеоморфности
- элементарное сродство, 1863). В начале 20 в. под влиянием развития теории множеств и аксиоматич. метода началось изучение Г. без предположений дифференцируемости. Такая задача, в явной форме впервые поставленная Д. Гильбертом (D. Hilbert) (см. [7], с. 31), составляет содержание пятой проблемы Гильберта. Особое значение имело установление Л. Брауэром (L. Brouwer) негомеоморфности  и
и 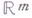 при
при  . Этим была восстановлена вера математиков в геометрич. интуицию, поколебленная результатами Г. Кантора (G. Kantor) о равно-мощности
. Этим была восстановлена вера математиков в геометрич. интуицию, поколебленная результатами Г. Кантора (G. Kantor) о равно-мощности 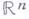 и
и 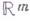 и Дж. Пеано (G. Рсаnо) о возможности непрерывного отображения
и Дж. Пеано (G. Рсаnо) о возможности непрерывного отображения 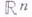 на
на  ,
, Введенные М. Фреше (М.
Введенные М. Фреше (М.  ) и Ф. Хаусдорфом (F. Hausdorf) понятия метрического (соответственно топологического) пространства поставили на прочный фундамент понятие Г. и позволили сформулировать понятия топологического свойства (свойства, не меняющегося при Г.), топологической инвариантности и т. п. и сформулировать задачу классификации топологич. пространств тех пли иных типов с точностью до Г. В такой постановке эта задача, однако, чрезвычайно сложна уже для очень узких классов пространств. Кроме классич. случая двумерных многообразий, классификация указана лишь для нек-рых видов графов, для двумерных полиэдров, для нек-рых классов многообразий. Алгоритмически проблема классификации в общем виде вообще неразрешима, так как невозможен алгоритм для различения, напр., многообразий размерности больше 3. Поэтому обычно задача о классификации ставится в рамках более слабого отношения эквивалентности, напр, в алгебраич. топологии для гомотопического типа или, наоборот, для классификации пространств, снабженных какой-либо структурой. В этом случае вопрос о Г. остается все же очень важным. В топологии многообразий лишь в конце 60-х гг. разработаны методы, позволяющие изучать многообразия с точностью до Г. При этом изучение проводится здесь в тесной связи гомотопической, топологической, кусочно линейной и гладкой структур.
) и Ф. Хаусдорфом (F. Hausdorf) понятия метрического (соответственно топологического) пространства поставили на прочный фундамент понятие Г. и позволили сформулировать понятия топологического свойства (свойства, не меняющегося при Г.), топологической инвариантности и т. п. и сформулировать задачу классификации топологич. пространств тех пли иных типов с точностью до Г. В такой постановке эта задача, однако, чрезвычайно сложна уже для очень узких классов пространств. Кроме классич. случая двумерных многообразий, классификация указана лишь для нек-рых видов графов, для двумерных полиэдров, для нек-рых классов многообразий. Алгоритмически проблема классификации в общем виде вообще неразрешима, так как невозможен алгоритм для различения, напр., многообразий размерности больше 3. Поэтому обычно задача о классификации ставится в рамках более слабого отношения эквивалентности, напр, в алгебраич. топологии для гомотопического типа или, наоборот, для классификации пространств, снабженных какой-либо структурой. В этом случае вопрос о Г. остается все же очень важным. В топологии многообразий лишь в конце 60-х гг. разработаны методы, позволяющие изучать многообразия с точностью до Г. При этом изучение проводится здесь в тесной связи гомотопической, топологической, кусочно линейной и гладкой структур.
Другая проблема состоит в топологической характер и заци и отдельных пространств и классов пространств (т. е. их указания характеристических топологич. свойств, формулируемых на языке аксиом топологии). Она решена, напр., для одномерных многобразий, двумерных многообразий, канторова множества, кривой Серпинского, кривой Менгера, псевдодуги, пространства Бэра и др. Универсальный метод для топологич. характеризации пространств дают спектры. С их помощью получена теорема Александрова о Г. (см. [4]). Последовательностью измельчающихся подразделений охарактеризована сфера и вообще класс локально евклидовых пространств (см. [5]). Посредством спектров дано описание локально бикомпактных групп (см. [6]). Другой метод состоит в рассмотрении различных алгебраич. структур, связанных с отображениями. Так, бикомпактное пространство совпадает с пространством максимальных идеалов алгебры действительных функций, заданных на нем.
Многие пространства характеризуются полугруппой непрерывных отображений в себя (см. Гомеоморфизмов группа). В общей топологии дается топологич. описание многих классов топологич. пространств. Представляет интерес также характеризация пространств внутри данного класса. Напр., очень полезно описание сферы как компактного многообразия, покрытого двумя открытыми клетками. Мало разработан вопрос об алгоритмич. распознавании пространств. Напр., он не решен (к 1977) для сферы
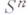 при
при 
Вообще, если два топологич. пространства негомеоморфны, то этот факт устанавливается указанием топологич. свойства, к-рым обладает лишь одно из них (компактность, связность и т. д.; напр., отрезок отличается от окружности тем, что он может быть разбит точкой); особое значение имеет здесь метод инвариантов. Инварианты определяются или аксиоматич. путем сразу для целого класса пространств, или алгоритмически, по конкретному представлению пространства, напр, по триангуляции, Хегора диаграмме, разложению на ручки и т. д. В первом случае возникает задача вычисления инварианта, во втором - доказательства топологич. инвариантности. Возможен и промежуточный случай, напр, характеристические классы гладких многообразий определялись сначала как препятствия к построению векторных и реперных полей, а затем стали определяться как образ касательного расслоения при преобразовании KO -функтора в когомологич. функтор, но в обоих случаях обе указанные задачи не решаются определением. Исторически первый пример доказательства топологич. инвариантности, именно, линейной размерности
 , дал Л. Брауэр (1912). Классический идущий от А. Пуанкаре метод состоит в том, чтобы дать сразу два определения: "вычислимое" и "инвариантное", и затем доказывать их совпадение. Этот прием оказался особенно успешным в теории гомологии полиэдров. Другой метод состоит в том, чтобы доказать, что инвариант не меняется при элементарных преобразованиях представления пространства (напр., подразделениях триангуляции). Он достигает цели, если известно, что таким образом можно получить все представления данного типа. В связи с этим, напр., в топологии полиэдра возникла т. н. основная гипотеза комбинаторной топологии. Этот метод (также идущий от А. Пуанкаре) оказался очень полезным в топологии двух и трех измерений, в частности в узлов теории, но он выходит из употребления (если не считать конструктивного направления) не столько в связи с тем, что указанная гипотеза оказалась неверной, сколько потому, что развитие теории категорий позволило давать определения, более отвечающие существу дела с более четкой постановкой задачи о вычислении и топологич. инвариантности. Так, инвариантность гомологии, определенных функториальным, но вычислимым образом для комплексов, следует из сравнения категорий комплексов и гомотопич. классов симплициальных отображений с категорией гомотопич. классов непрерывных отображений, что позволяет не давать отдельного определения для большей категории, а распространить его с меньшей. (Истоки этой идеи содержатся в теории степени Брауэ-ра.) Особенно ярко преимущество нового метода проявилось в связи с указанным выше вторым определением характернстич. классов как преобразований функторов. Так, напр., вопрос о топологич. инвариантности естественным образом оказался частью вопроса о соотношении между K-функтором и его топологич. обобщением.
, дал Л. Брауэр (1912). Классический идущий от А. Пуанкаре метод состоит в том, чтобы дать сразу два определения: "вычислимое" и "инвариантное", и затем доказывать их совпадение. Этот прием оказался особенно успешным в теории гомологии полиэдров. Другой метод состоит в том, чтобы доказать, что инвариант не меняется при элементарных преобразованиях представления пространства (напр., подразделениях триангуляции). Он достигает цели, если известно, что таким образом можно получить все представления данного типа. В связи с этим, напр., в топологии полиэдра возникла т. н. основная гипотеза комбинаторной топологии. Этот метод (также идущий от А. Пуанкаре) оказался очень полезным в топологии двух и трех измерений, в частности в узлов теории, но он выходит из употребления (если не считать конструктивного направления) не столько в связи с тем, что указанная гипотеза оказалась неверной, сколько потому, что развитие теории категорий позволило давать определения, более отвечающие существу дела с более четкой постановкой задачи о вычислении и топологич. инвариантности. Так, инвариантность гомологии, определенных функториальным, но вычислимым образом для комплексов, следует из сравнения категорий комплексов и гомотопич. классов симплициальных отображений с категорией гомотопич. классов непрерывных отображений, что позволяет не давать отдельного определения для большей категории, а распространить его с меньшей. (Истоки этой идеи содержатся в теории степени Брауэ-ра.) Особенно ярко преимущество нового метода проявилось в связи с указанным выше вторым определением характернстич. классов как преобразований функторов. Так, напр., вопрос о топологич. инвариантности естественным образом оказался частью вопроса о соотношении между K-функтором и его топологич. обобщением.
Еслп два пространства гомеоморфны, то для установления Г. общее значение имеет лишь метод спектров (и измельчающихся подразделений). С другой стороны, в том случае, когда построена классификация, вопрос решается сравнением инвариантов. На практике установление Г. часто оказывается очень трудной геометрич. задачей, к-рую приходится решать специальными средствами. Так, Г. евклидова пространства и нек-рых его факторпространств устанавливается с помощью псевдоизотопии.
Лит.:[1]Гильберт Д., Кон -Фоссен С., Наглядная геометрия, пер. с нем., 2 изд., М.-Л., 1951; [2] Болтянский В. Г., Ефремович В. А., "Матем. просвещение", 1957, вып. 2; [3] Пуанкаре А., Собр. соч., пер. с франц., т. 2, М., 1972; [4] Александров П. С., "Тр. Матем. ин-та. АН СССР", 1959, т. 54, с. 1-136; [5] Наrrо1d О. G., "Trans. Amer. Math. Soc.", 1965, v. 118, №6, p. 1-16; [6] Понтрягин Л. С., Непрерывные группы, 3 изд., М., 1973; [7] Проблемы Гильберта, М., 1969. А. В. Чернавский.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
