ГИЛЬБЕРТА МНОГОЧЛЕН

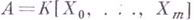градуированного модуля - многочлен, выражающий при больших натуральных празмерности однородных слагаемых модуля как функцию от п. Более точно, справедлива теорема, доказанная по существу Д. Гильбертом. Пусть - кольцо многочленов над полем К, градуированное так, что являются однородными элементами степени 1, н пусть - градуированный A-модуль конечного типа; тогда существует такой многочлен с рациональными коэффициентами, что для достаточно больших п 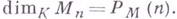Этот многочлен наз. многочленом Гильберта.

Наибольший интерес представляет интерпретация Г. м. градуированного кольца R, являющегося фактор-кольцом кольца А по однородному идеалу I; в этом случае Г. м. доставляет проективные инварианты проективного многообразия 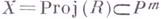, определя мого идеалом I. В частности, степень многочлена 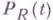совпадает с размерностью многообразия X, а 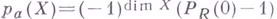наз. арифметическим родом многообразия X. Через Г. м. выражается также степень вложения 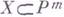. Г. м. кольца R называют также Г. м. проективного многообразия Xотносительно вложения 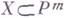. Если 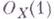- обратимый пучок, соответствующий этому вложению, то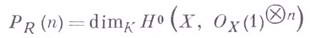

для достаточно больших п.

Лит.:[1] Нi1bеrt D., Gesammelte Abhandlungen, Bd 2, В., 1933; [2] Бальдассарри М., Алгебраические многообразия, пер. с англ., М., 1961; [3] Зарисский О., Самюэль П., Коммутативная алгебра, т. 2, пер. с англ., М., 1963. В. И. Данилов.