ГЁДЕЛЯ ИНТЕРПРЕТАЦИЯ

интуиционистской арифметики - специальная операция, переводящая формулы интуиционистской арифметики в формулы вида где - наборы переменных по вычислимым функциям специального вида. При этом выводимые формулы переводятся в истинные формулы в смысле нек-рои четко описанной семантики. Эта интерпретация, к-рая была использована К. Гёделем для нового доказательства непротиворечивости арифметики формальной, представляет также значительный интерес как нек-рая семантика для языка формальной арифметики.

Рассматривается бескванторная аксиоматич. теория Тс бесконечным числом типов переменных. Класс переменных данного типа определяется индуктивно, а именно: 1) - переменные типа 0, переменные для натуральных чисел; 2) пусть теория содержит переменные типов тогда теория содержит и переменные типа t, где tесть . Переменные типа tобозначаются через и рассматриваются как переменные для вычислимых в нек-ром смысле функций, перерабатывающих каждый набор функций типов соответственно в функцию типа . Язык Тсодержит термы различных типов: переменная типа является термом типа , 0 есть терм типа О, символ s, к-рый служит для обозначения функции прибавления единицы к натуральному числу, есть терм типа (0,0). Остальные термы образуются с помощью правил порождения: Черча -абстракции и примитивной рекурсии для функций произвольного типа. Атомарные формулы теории Тсуть равенства , где - термы типа 0. Формулы теории Тполучаются из атомарных с помощью логических связок исчисления высказываний . Постулатами Тявляются аксиомы и правила вывода интуиционистского исчисления высказываний, аксиомы для равенства, аксиомы Пеано для 0 и S, уравнения примитивных рекурсий, аксиома применения функции, определенной l-абстракцией, и, наконец, принцип математич. индукции, сформулированный в виде правила вывода без употребления кванторов. Через обозначим теорию Т, пополненную кванторами по переменным произвольного типа и соответствующими логическими аксиомами и правилами вывода для кванторов.

Г. и. переводит всякую формулу (а следовательно, и всякую формулу интуиционистской арифметики) в формулу вида

где - формула без кванторов, а - наборы переменных различных типов, - совокупность всех свободных переменных формулы .

Пусть F - формула интуиционистской арифметики и - ее гёделевская интерпретация. Если Fвыводима в формальной интуиционистской арифметике, то может быть построен терм теории Ттакой, что формула 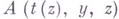выводима в Т. Таким образом, непротиворечивость арифметики сводится к установлению непротиворечивости бескванторной теории Т.

Интуиционистская семантика на основе Г. и. определяется следующим образом: формула Fсчитается истинной, если найдется вычислимый терм такой, что бескванторная формула истинна при всяком вычислимом z.

Лит.:[1]Гёдель К., в сб.: Математическая теория логического вывода, М., 1967, с. 299-310. А. Г. Драгалин.