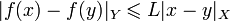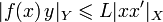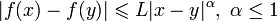- Гёльдера условие
-
Липшицево отображение — отображение
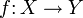 между метрическими пространствами X и Y, удовлетворяющее условию
между метрическими пространствами X и Y, удовлетворяющее условиюДля некоторой вещественной константы L и всех
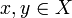 . Здесь
. Здесь 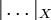 обозначает метрику в пространстве X. Это условие часто называют условием Липшица.
обозначает метрику в пространстве X. Это условие часто называют условием Липшица.Содержание
Связанные определения
- Отображение, удовлетворяющее вышеприведённому условию, называется также L-липшицевым.
- 1-липшицево отображение называют также коротким отображением
- Нижняя грань чисел L, удовлетворяющих вышеприведённому неравенству, назывется константой Липшица отображения f.
- Отображение
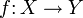 называется билипшицевым, если у него существует обратное
называется билипшицевым, если у него существует обратное 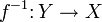 и оба f и f − 1 являются липшицевыми
и оба f и f − 1 являются липшицевыми - Отображение
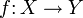 называется колипшицевым, если существует константа L, такая, что для любых
называется колипшицевым, если существует константа L, такая, что для любых  и
и 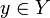 найдётся
найдётся 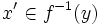 такое, что
такое, что
Свойства
- Любое отображение Липшица равномерно непрерывно.
Вариации и обобщения
- Понятие липшицевой функции естественным образом обобщается на функции с ограниченным модулем непрерывности, так как условие Липшица записывается так:
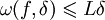 .
.
История
Отображения с со свойством
впервые рассматривалось Липшицем в 1864 для вещественных функций, в качестве достаточного условия для сходимости ряда Фурье к своей функции. В последствии условием Липшица стало принято называть это условие только при α = 1, а при α < 1 условием Гёльдера.
См. также
Wikimedia Foundation. 2010.