- ГЁЛЬДЕРА УСЛОВИЕ
- неравенство, в к-ром приращение функции оценивается через приращение ее аргумента. Функция
, определенная в области Е n -мерного евклидова пространства, удовлетворяет в точке 
Г. у. с показателем 
(порядка 
), где 
, и коэффициентом (у), если
для всех
, достаточно близких к у. Это Г. у. наз. иногда изотропным Г. у. Говорят, что 
удовлетворяет на множестве 
(изотропному) Г. у. с показателем 
, если Г. у. (1) выполнено для всех 
. В случае, когда
Г. у. наз. равномерным на
, а 
- коэффициентом Гёльдера функции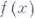 
на Е. Т. у. наз. также непрерывностью по Гельдеру. Величина
наз.
-полунормой Гёльдера ограниченной функции на множестве Е. Полунорма Гёльдера, как функция от f, логарифмически выпукла:
Неизотропное Г. у. вводится аналогично Г. у. (1) и имеет вид:
где
, а 
. Функции, удовлетворяющие неизотропному Г. у., непрерывны и имеют по направлению ковектора 
показатель Гёльдера 
.
Для числовых функций одного действительного переменного условие вида (1) было введено Р. Липшицем (R. l.ipschitz, 1864) в связи с исследованиями но тригонометрич. рядам. В этом случае Г. у. часто наз. условием Липшица порядка
с константой Липшица А. Для числовых функций 
действительных переменных Г. у. было введено О. Гёльдером 
при исследовании дифференциальных свойств ньютонова потенциала.
Г. у. естественным образом переносится на случай отображений метрич. пространств. Говорят, что отображение
метрич. пространства Xв метрич. пространство 
удовлетворяет в точке 
Г. у. с показателем 
и коэффициентом 
если, существует такая окрестность 
точки 
, что для любого 
выполняется неравенство
Здесь
и 
- метрики пространств 
. Аналогично вводится Г. у. на множестве 
, равномерное на XГ. у. и 
- полунормы Гёльдера.
Векторные пространства функций, удовлетворяющих тому или иному Г. у., образуют Гёльдерово пространство, л. П. Купцов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
