Λ-исчисление

Ля́мбда-исчисле́ние (λ-исчисление, лямбда-исчисление) — формальная система, разработанная американским математиком Алонзо Чёрчем, для формализации и анализа понятия вычислимости.

λ-исчисление может рассматриваться как семейство прототипных языков программирования. Их основная особенность состоит в том, что они являются языками высших порядков. Тем самым обеспечивается систематический подход к исследованию операторов, аргументами которых могут быть другие операторы, а значением также может быть оператор. Языки в этом семействе являются функциональными, поскольку они основаны на представлении о функции или операторе, включая функциональную аппликацию и функциональную абстракцию.

λ-исчисление реализовано Джоном Маккарти в языке Лисп. В начале реализация идей λ-исчисления была весьма громоздкой. Но по мере развития Лисп-технологии (прошедшей этап аппаратной реализации в виде Лисп-машины) идеи получили ясную и четкую реализацию.

Чистое λ-исчисление

Это простейший из семейства прототипных языков программирования, чистое λ-исчисление, термы которого, называемые также объектами (обами), или λ-термами, построены исключительно из переменных применением аппликации и абстракции. Изначально наличия каких-либо констант не предполагается.

Аппликация и абстракция

В основу λ-исчисления положены две фундаментальные операции: аппликация и абстракция. Аппликация означает применение или вызов функции по отношению к заданному значению. Её обычно обозначают 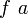$f\ a$, где f — функция, а a — значение. Это соответствует общепринятой в математике записи f(a), которая тоже иногда используется, однако для λ-исчисления важно то, что f трактуется как алгоритм, вычисляющий результат по заданному входному значению. В этом смысле аппликация f к a может рассматриваться двояко: как результат применения f к a, или же как процесс вычисления 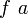$f\ a$. Последняя интерпретация аппликации связана с понятием β-редукции.

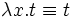Абстракция или λ-абстракция в свою очередь строит функции по заданным выражениям. Именно, если $t\equiv t[x]$ — выражение, свободно содержащее x, тогда $\ \lambda x.t[x]$ обозначает функцию $x\mapsto t[x]$. Таким образом, с помощью абстракции можно конструировать новые функции. Требование, чтобы x свободно входило в t, не очень существенно — достаточно предположить, что $\lambda x.t\equiv t$, если это не так.

β-редукция

Поскольку выражение 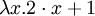$\lambda x. 2\cdot x + 1$ обозначает функцию, ставящую в соответствие каждому x значение 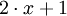$2\cdot x + 1$, то для вычисления выражения

$(\lambda x. 2\cdot x + 1)\ 3$,

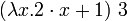в которое входят и аппликация и абстракция, необходимо выполнить подстановку числа 3 в терм 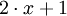$2\cdot x + 1$. В результате получается 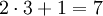$2\cdot 3+1=7$. Это соображение в общем виде записывается как

$(\lambda x.t)\ a = t[x:=a],$

и носит название β-редукция. Выражение вида 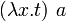$(\lambda x.t)\ a$, то есть применение абстракции к некому терму, называется редексом (redex). Несмотря на то, что β-редукция по сути является единственной «существенной» аксиомой λ-исчисления, она приводит к весьма содержательной и сложной теории. Вместе с ней λ-исчисление обладает свойством полноты по Тьюрингу и, следовательно, представляет собой простейший язык программирования.

η-преобразование

η-преобразование выражает ту идею, что две функции являются идентичными тогда и только тогда, когда, будучи применённые к любому аргументу, дают одинаковые результаты. η-преобразование переводит друг в друга формулы 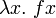$\lambda x.\ f x$ и f (в обратную сторону — только если x не имеет свободных вхождений в f: иначе свободная переменная x после преобразования станет связанной внешней абстракцией).

Надо отметить, что если рассматривать лямбда-термы не как функции, а именно как алгоритмы, то данное преобразование не всегда уместно: существуют случаи, когда вычисление 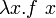$\lambda x. f\ x$ завершается, а вычисление f не завершается.

Каррирование (карринг)

Функция двух переменных x и y f(x,y) = x + y может быть рассмотрена как функция одной переменной x, возвращающая функцию одной переменной y, то есть как выражение 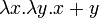$\ \lambda x.\lambda y.x+y$. Такой приём работает точно также для функций любой арности. Это показывает, что функции многих переменных могут быть без проблем выражены в λ-исчислении и являются «синтаксическим сахаром». Описанный процесс превращения функций многих переменных в функцию одной переменной называется карринг (также: каррирование), в честь американского математика Хаскелла Карри, хотя первым его предложил М. И. Шейнфинкель (1924).

Семантика бестипового λ-исчисления

Тот факт, что термы λ-исчисления действуют как функции, применяемые к термам λ-исчисления (то есть, возможно, к самим себе) приводит к сложностям построения адекватной семантики λ-исчисления. Можно ли приписать λ-исчислению какой-либо смысл? Желательно иметь множество D, в которое вкладывалось бы его пространство функций D → D. В общем случае такого D не существует по соображениям ограничений на мощности этих двух множеств, D и функций из D в D: второе имеет большую мощность, чем первое.

Эту трудность преодолел Д.С. Скотт, построив понятие области D (полной решётки^[1] или, более общо, полного частично упорядоченного множества со специальной топологией) и урезав D → D до непрерывных (в имеющейся топологии) функций^[2]. После этого также стало понятно, как можно строить денотационную семантику языков программирования. Это произошло благодаря тому, что с помощью конструкций Скотта можно придать значение также двум важным конструкциям языков программирования — рекурсии и типам данных.

Связь с рекурсивными функциями

См. также

• Аппликативные вычислительные системы
• Типизированное λ-исчисление
• Комбинаторная логика
• Функциональное программирование

Ссылки

1. ↑ Scott D.S. The lattice of flow diagrams.-- Lecture Notes in Mathematics, 188, Symposium on Semantics of Algorithmic Languages.-- Berlin, Heidelberg, New York: Springer-Verlag, 1971, pp. 311-372.
2. ↑ Scott D.S. Lattice-theoretic models for various type-free calculi. -- In: Proc. 4th Int. Congress for Logic, Methodology, and the Philosophy of Science, Bucharest, 1972.

Литература

• Барендрегт X. Ламбда-исчисление. Его синтаксис и семантика: Пер. с англ. — М.: Мир, 1985. — 606 с.