Решение треугольников

Решение треугольников (лат. solutio triangulorum) — исторический термин, означающий решение главной тригонометрической задачи: по известным данным о треугольнике (стороны, углы и т. д.) найти остальные его характеристики^[1]. Треугольник может располагаться на плоскости или на сфере. Данная задача часто встречается в тригонометрических приложениях, например, в геодезии, астрономии, строительстве, навигации.

Решение плоских треугольников

Стандартные обозначения в треугольнике

У треугольника общего вида имеется 6 основных характеристик: 3 линейные (длины сторон $a, b, c$) и 3 угловые ($\alpha, \beta. \gamma$), см. рисунок. В классической задаче плоской тригонометрии заданы 3 из этих 6 характеристик, и нужно определить 3 остальные. Очевидно, если известны только 2 или 3 угла, однозначного решения не получится, так как любой треугольник, подобный данному, тоже будет решением, поэтому будем считать, что хотя бы одна из известных величин — линейная.

Алгоритм решения задачи зависит от того, какие именно характеристики треугольника считаются известными. Далее будем символически обозначать заданные величины С (сторона) и У (угол). Поскольку сочетание УУУ исключено из рассмотрения, остаются 5 различных вариантов^[2]:

• Три стороны (ССС);
• Две стороны и угол между ними (СУС);
• Две стороны и угол не между ними (ССУ);
• Сторона и два прилежащих угла (УСУ);
• Сторона, противолежащий угол и один из прилежащих (УУС).

Основные теоремы

Стандартным методом решения задачи является использование нескольких фундаментальных соотношений, выполняющихся для всех плоских треугольников:

Теорема косинусов

$a^2 = b^2 + c^2 - 2 b c \cos \alpha$

$b^2 = a^2 + c^2 - 2 a c \cos \beta$

$c^2 = a^2 + b^2 - 2 a b \cos \gamma$

Теорема синусов

$\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma}$

Сумма углов треугольника

$\alpha + \beta + \gamma = 180^\circ$

Теорема тангенсов (применяется редко)

$\frac{a-b}{a+b} = \frac{\mathrm{tg}[\frac{1}{2}(\alpha-\beta)]}{\mathrm{tg}[\frac{1}{2}(\alpha+\beta)]}.$

Из других, иногда полезных на практике универсальных соотношений, следует упомянуть теорему котангенсов и формулы Мольвейде.

Замечания

1. Для нахождения неизвестного угла надёжнее использовать теорему косинусов, а не синусов. Причина в том, что значение синуса угла при вершине треугольника не определяет однозначно самого угла — например, если $\sin \beta = 0{,}5,$ то угол $\beta$ может быть как $30^\circ$, так и $150^\circ$ (синусы этих углов совпадают). С косинусом такие проблемы не возникают, в интервале от $0^\circ$ до $180^\circ$ значение косинуса определяет угол однозначно.
2. Далее всюду предполагается, что взаимное расположение заданных характеристик треугольника известно; если это не так, то зеркальное отражение построенного треугольника тоже будет решением задачи. Например, три стороны однозначно определяют треугольник с точностью до отражения.

Заданы три стороны

Три стороны

Пусть заданы длины всех трёх сторон $a, b, c$. Чтобы найти углы $\alpha, \beta$, воспользуемся теоремой косинусов^[3]:

$\alpha = \arccos \frac{b^2 + c^2 - a^2} {2 b c}$

$\beta = \arccos \frac{a^2 + c^2 - b^2} {2 a c}$

Третий угол сразу находится из правила, что сумма всех трёх углов должна быть равна 180°.

В некоторых источниках предлагается второй угол найти по теореме синусов, но, как указано в вышеприведенном замечании 1, при этом существует опасность спутать тупой угол с острым.

Ещё один метод вычисления углов по известным сторонам: использование теоремы котангенсов.

Заданы две стороны и угол между ними

Две стороны и угол между ними

Пусть, для определённости, известны длины сторон $a, b$ и угол $\gamma$ между ними. Для определения длины стороны $c$ вновь воспользуемся теоремой косинусов^[4]:

$c = \sqrt{a^2+b^2-2ab\cos\gamma}$

Мы фактически свели задачу к предыдущему случаю. Далее воспользуемся теоремой косинусов для нахождения второго угла:

$\alpha = \arccos \frac{b^2 + c^2 - a^2} {2 b c}$

Третий угол $\beta = 180^\circ - \alpha - \gamma$.

Заданы две стороны и угол не между ними

Две стороны и угол не между ними

Этот случай самый сложный и неоднозначный. Пусть, например, известны две стороны $b, c$ и угол $\beta$. Уравнение для угла $\gamma$ найдём из теоремы синусов^[5]:

$\sin\gamma = \frac{c}{b} \sin\beta$

Для краткости обозначим $~D=\frac{c}{b} \sin\beta$ (правая часть уравнения). При решении уравнения возможны 4 случая^[6].

1. Если $D>1$, такого треугольника не существует (сторона $b$ «не достаёт» до линии BC).
2. Если $D=1$, существует единственное решение, причём треугольник прямоугольный, $\gamma = 90^\circ$.

Два возможных решения

3. Если $D<1$, то возможны 2 варианта.
   1. Если $b<c$, то угол $\gamma$ имеет два возможных значения: острый угол $~\gamma = \arcsin D$ и тупой угол $~\gamma' = 180^\circ - \gamma$. На рисунке справа первому значению соответствуют точка $C$, сторона $b$ и угол $\gamma$, а второму значению — точка $C'$, сторона $b'$ и угол $\gamma'$.
   2. Если $b \geqslant c$, то $\beta \geqslant \gamma$ (как известно, большей стороне треугольника соответствует больший противолежащий угол). Поскольку в треугольнике не может быть двух тупых углов, тупой угол для $~\gamma$ исключён, и решение $~\gamma=\arcsin D$ единственно.

Третий угол находится как обычно: $\alpha = 180^\circ - \beta - \gamma$. Третью сторону можно найти по теореме синусов:

$a = b\ \frac{\sin\alpha}{\sin\beta}$

Заданы сторона и прилежащие к ней углы

Сторона и прилежащие к ней углы

Пусть задана сторона $c$ и углы $\alpha, \beta$. Вначале находим третий угол $~\gamma = 180^\circ - \alpha - \beta$. Далее обе неизвестные стороны находятся по теореме синусов^[7]:

$a = c\ \frac{\sin\alpha}{\sin\gamma}; \quad b = c\ \frac{\sin\beta}{\sin\gamma}$

Сторона, прилежащий и противолежащий углы

Этот случай решается так же, как предыдущий: находим третий угол и применяем теорему синусов.

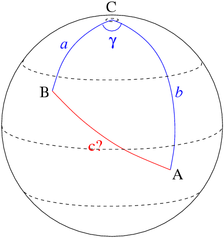
Решение сферических треугольников

Сферический треугольник общего вида полностью определяется тремя из шести своих характеристик (3 стороны и 3 угла). Отметим, что стороны сферического треугольника $a, b, c$ принято измерять не линейными единицами, а величиной опирающихся на них центральных углов.

Решение треугольников в неевклидовой сферической геометрии имеет ряд отличий от плоского случая. Например, сумма трёх углов $\alpha+\beta+\gamma$ зависит от треугольника; кроме того, на сфере не существует неравных подобных треугольников, и поэтому задача построения треугольника по трём углам имеет единственное решение. Но базовые соотношения, используемые для решения задачи, аналогичны плоскому случаю: теоремы косинусов (сферическая геометрия) и теорема синусов (сферическая геометрия).

Из других соотношений могут оказаться полезными формулы аналогии Непера и формула половины стороны.

Заданы три стороны

Три стороны

Если заданы стороны $a, b, c$ (напомним, в угловых единицах), то углы треугольника определяются из теоремы косинусов:

$\alpha = \arccos\left(\frac{\cos a-\cos b\ \cos c}{\sin b\ \sin c}\right)$,

$\beta = \arccos\left(\frac{\cos b-\cos c\ \cos a}{\sin c\ \sin a}\right)$,

$\gamma = \arccos\left(\frac{\cos c-\cos a\ \cos b}{\sin a\ \sin b}\right)$,

Заданы две стороны и угол между ними

Две стороны и угол между ними

Пусть заданы стороны $a, b$ и угол $\gamma$ между ними. Сторону $c$ легко найти по теореме косинусов:

$c = \arccos \left(\cos a\cos b + \sin a\sin b\cos\gamma \right)$

Углы $\alpha, \beta$ можно найти так же, как в предыдущем варианте, можно также использовать формулы аналогии Непера:

$\alpha = \operatorname{arctg}\ \frac{2\sin a}{\operatorname{tg}(\frac{\gamma}{2}) \sin (b+a) + \operatorname{ctg}(\frac{\gamma}{2})\sin(b-a)}$

$\beta = \operatorname{arctg}\ \frac{2\sin b}{\operatorname{tg}(\frac{\gamma}{2}) \sin (a+b) + \operatorname{ctg}(\frac{\gamma}{2})\sin(a-b) }$,

Заданы две стороны и угол не между ними

Две стороны и угол не между ними

Пусть заданы стороны $b, c$ и угол $\beta$. Чтобы решение существовало, необходимо выполнение условия:

$b > \arcsin (\sin c\,\sin\beta)$

Угол $\gamma$ получается из теоремы синусов:

$\gamma = \arcsin \left(\frac{\sin c\,\sin\beta}{\sin b}\right)$

Здесь, аналогично плоскому случаю, при $b>c$ получаем два решения: $\gamma$ и $~180^\circ - \gamma$.

Остальные величины можно найти из формул аналогии Непера:

$a = 2\operatorname{arctg} \left\{ \operatorname{tg}\left(\frac12(b-c)\right) \frac{\sin \left(\frac12(\beta+\gamma)\right)}{\sin\left(\frac12(\beta-\gamma)\right)} \right\}$,

$\alpha = 2\operatorname{arcctg} \left\{\operatorname{tg}\left(\frac12(\beta-\gamma)\right) \frac{\sin \left(\frac12(b+c)\right)}{\sin \left(\frac12(b-c)\right)} \right\}$.

Заданы сторона и прилежащие углы

Сторона и прилежащие углы

В этом варианте задана сторона $c$ и углы $\alpha, \beta$. Найдём угол $\gamma$ по теореме косинусов:

$\gamma = \arccos(\sin\alpha\sin\beta\cos c -\cos\alpha\cos\beta)\,$,

Две неизвестные стороны получаем из формул аналогии Непера:

$a = \operatorname{arctg}\left\{\frac{2\sin\alpha}{\operatorname{ctg}(c/2) \sin(\beta+\alpha) + \operatorname{tg}(c/2) \sin(\beta-\alpha)}\right\}$

$b = \operatorname{arctg}\left\{\frac{2\sin\beta} {\operatorname{ctg}(c/2) \sin(\alpha+\beta) + \operatorname{tg}(c/2)\sin(\alpha-\beta)}\right\}$

или, используя вычисленный угол $\gamma$, по теореме косинусов:

$a=\arccos\left(\frac{\cos\alpha+\cos\beta\cos\gamma}{\sin\beta\sin\gamma}\right)$

$b=\arccos\left(\frac{\cos\beta+\cos\gamma\cos\alpha}{\sin\gamma\sin\alpha}\right)$

Заданы два угла и сторона не между ними

Два угла и сторона не между ними

Пусть заданы сторона $a$ и углы $\alpha, \beta$. Сторону $b$ найдём по теореме синусов:

$b = \arcsin \left( \frac{\sin a\,\sin \beta}{\sin \alpha} \right)$,

Если угол для стороны $a$ острый и $\alpha > \beta$, существует второе решение:

$b = \pi - \arcsin \left( \frac{\sin a\,\sin \beta}{\sin \alpha} \right)$

Остальные величины определим из формул аналогии Непера:

$c = 2\operatorname{arctg} \left\{ \operatorname{tg}\left(\frac12(a-b)\right) \frac{\sin\left(\frac12(\alpha+\beta)\right)}{\sin\left(\frac12(\alpha-\beta)\right)}\right\}$,

$\gamma = 2\operatorname{arcctg} \left\{\operatorname{tg}\left(\frac12(\alpha-\beta)\right) \frac{\sin \left(\frac12(a+b)\right)}{\sin \left(\frac12(a-b)\right)} \right\}$,

Заданы три угла

Три угла

Если заданы три угла, стороны находятся по теореме косинусов:

$a=\arccos\left(\frac{\cos\alpha+\cos\beta\cos\gamma}{\sin\beta\sin\gamma}\right)$,

$b=\arccos\left(\frac{\cos\beta+\cos\gamma\cos\alpha}{\sin\gamma\sin\alpha}\right)$,

$c=\arccos\left(\frac{\cos\gamma+\cos\alpha\cos\beta}{\sin\alpha\sin\beta}\right)$.

Решение прямоугольных сферических треугольников

Изложенные алгоритмы значительно упрощаются, если известно, что один из углов треугольника (скажем, угол $C$) прямой. Прямоугольный сферический треугольник полностью определяется двумя элементами, остальные три находятся при помощи мнемонического правила Непера или из нижеприведенных соотношений.

$\sin a = \sin c \cdot \sin A$ (частный случай сферической теоремы синусов)

$\operatorname{tg} a = \sin b \cdot \operatorname{tg} A$

$\cos c = \cos a \cdot \cos b$ (частный случай сферической теоремы косинусов)

$\operatorname{tg} b = \operatorname{tg} c \cdot \cos A$

$\cos A = \cos a \cdot \sin B$ (тоже вытекает из сферической теоремы косинусов)

$\cos c = \operatorname{ctg} A \cdot \operatorname{ctg} B$

Вариации и обобщения

Во многих практически важных задачах вместо сторон треугольника задаются другие его характеристики — например, длина медианы, высоты, биссектрисы, радиус вписанного или описанного круга и т. д. Аналогично вместо углов при вершинах треугольника в задаче могут фигурировать иные углы. Алгоритмы решения подобных задач чаще всего комбинируется из рассмотренных выше теорем тригонометрии.

Примеры:

• Задача Региомонтана: построить треугольник, если известны одна его сторона, длина опущенной на неё высоты и противолежащий угол^[8].
• Задача Снеллиуса-Потно́ (англ.)русск.
• Задача Томаса Финке: найти углы треугольника, если известна сумма двух углов $\alpha+\beta$ и отношение противолежащих сторон $a:b$^[9].
• Задача Ньютона: решить треугольник, если известны одна его сторона, противолежащий угол и сумма двух других сторон.

Примеры практического применения

Триангуляция

Определение расстояния с помощью триангуляции

Основная статья: Триангуляция (геодезия)

Чтобы определить расстояние $d$ от берега до удалённого корабля, нужно отметить на берегу две точки, расстояние $l$ между которыми известно. Измерим углы $\alpha$ и $\beta$ между линией, соединяющей эти точки, и направлением на корабль. Из формул варианта «сторона и прилежащие к ней углы» несложно найти длину высоты треугольника:

$d = \frac{\sin\alpha\,\sin\beta}{\sin(\alpha+\beta)} \,l = \frac{\operatorname{tg}\alpha\,\operatorname{tg}\beta}{\operatorname{tg}\alpha+\operatorname{tg}\beta} \,l$

Этот метод используется в каботажном судоходстве. Углы $\alpha, \beta$ при этом оцениваются наблюдениями с корабля известных ориентиров на земле.

Определение высоты горы

Другой пример: требуется измерить высоту $h$ горы или высокого здания. Известны углы $\alpha, \beta$ наблюдения вершины из двух точек, расположенных на расстоянии $l$. Из формул того же варианта, что и выше, получаем:

$h = \frac{\sin\alpha\,\sin\beta}{\sin(\beta-\alpha)} \,l = \frac{\operatorname{tg}\alpha\,\operatorname{tg}\beta}{\operatorname{tg}\beta-\operatorname{tg}\alpha} \,l$

Расстояние между двумя точками на земном шаре

Надо вычислить расстояние между двумя точками на земном шаре:

Точка A: широта $\lambda_\mathrm{A},$ долгота $L_\mathrm{A},$

Точка B: широта $\lambda_\mathrm{B},$ долгота $L_\mathrm{B},$

Рассмотрим сферический треугольник $ABC$, где $C$ — северный полюс. Для него известны следующие величины:

$a = 90^\mathrm{o} - \lambda_\mathrm{B}\,$

$b = 90^\mathrm{o} - \lambda_\mathrm{A}\,$

$\gamma = L_\mathrm{A}-L_\mathrm{B}\,$

Это случай «две стороны и угол между ними». Из приведенных там формул получаем:

$\mathrm{AB} = R \arccos\left\{\sin \lambda_\mathrm{A} \,\sin \lambda_\mathrm{B} + \cos \lambda_\mathrm{A} \,\cos \lambda_\mathrm{B} \,\cos \left(L_\mathrm{A}-L_\mathrm{B}\right)\right\}$,

Здесь $R$ — радиус Земли.

История

Основная статья: История тригонометрии

Зачатки тригонометрических знаний можно найти в математических рукописях древнего Египта, Вавилона и древнего Китая. Главным достижением этого периода стало соотношение, позже получившее имя теоремы Пифагора; Ван дер Варден считает, что вавилоняне открыли его между 2000 и 1786 годами до н. э.^[10].

Общая постановка задачи решения треугольников (как плоских, так и сферических) появилась в древнегреческой геометрии^[11]. Во второй книге «Начал» Евклида теорема 12 представляет собой словесный аналог теоремы косинусов^[12]:

В тупоугольных треугольниках квадрат на стороне, стягивающей тупой угол, больше [суммы] квадратов на сторонах, содержащих тупой угол, на дважды взятый прямоугольник, заключённый между одной из сторон при тупом угле, на которую падает перпендикуляр, и отсекаемым этим перпендикуляром снаружи отрезком при тупом угле.

Следующая за ней теорема 13 — вариант теоремы косинусов для остроугольных треугольников. Аналога теоремы синусов у греков не было, это важнейшее открытие было сделано гораздо позднее^[13].

Первые тригонометрические таблицы составил, вероятно, Гиппарх в середине II века до н. э. для астрономических расчётов. Позднее астроном II века Клавдий Птолемей в «Альмагесте» дополнил результаты Гиппарха. Тринадцать книг «Альмагеста» — самая значимая тригонометрическая работа всей античности. В частности, «Альмагест» содержит обширные пятизначные тригонометрические таблицы для острых и тупых углов, с шагом 30 угловых минут^[1].

Параллельно с развитием тригонометрии плоскости греки, под влиянием астрономии, далеко продвинули сферическую тригонометрию^[14]). Решающим этапом в развитии теории стала монография «Сферика» в трёх книгах, которую написал Менелай Александрийский (около 100 года н. э.). В первой книге он изложил теоремы о сферических треугольниках, аналогичные теоремам Евклида о плоских треугольниках (см. I книгу «Начал»). По сообщению Паппа, Менелай первым ввёл понятие сферического треугольника как фигуры, образованной отрезками больших кругов^[15]. Несколько десятилетий спустя Клавдий Птолемей в своих трудах «География», «Аналемма» и «Планисферий» даёт подробное изложение тригонометрических приложений к картографии, астрономии и механике.

В IV веке, после гибели античной науки, центр развития математики переместился в Индию. Сочинения индийских математиков (сиддханты) показывают, что их авторы были хорошо знакомы с трудами греческих астрономов и геометров^[16]. Чистой геометрией индийцы интересовались мало, но их вклад в прикладную астрономию и расчётные аспекты тригонометрии очень значителен. В частности, индийцы первыми ввели в использование косинус^[17]. Важный вклад в развитие тригонометрии внес Брахмагупта (VII в.), открывший несколько тригонометрических соотношений, в том числе и те, которые в современной записи приняли вид^[18]:

$\sin^2 \alpha + \cos^2 \alpha = 1$

$\sin\alpha = \cos(90^\circ - \alpha)$

Кроме того, индийцы знали формулы для кратных углов $\sin n\varphi$, $\cos n\varphi$ для $n = 2, 3, 4, 5$. В «Сурья-сиддханте» и в трудах Брахмагупты при решении задач фактически используется сферический вариант теоремы синусов, однако общая формулировка этой теоремы в Индии так и не появилась^[19]. В трудах другого выдающегося ученого, Бхаскары II (XII век), приводятся формулы для синуса и косинуса суммы и разности углов:

$\sin (\alpha \pm \beta) = \sin\alpha \cos\beta \pm \cos\alpha \sin\beta,$

а также формула для малого приращения синуса:

$\sin \alpha - \sin \beta \approx (\alpha - \beta)\cos \beta$

(при $\alpha \approx \beta$), соответствующая современному выражению для дифференциала синуса.

В VIII веке учёные стран Ближнего и Среднего Востока познакомились с трудами древнегреческих и индийских математиков и астрономов. Их астрономические трактаты, аналогичные индийским сиддхантам, назывались «зиджи»; типичный зидж представлял собой сборник астрономических и тригонометрических таблиц, снабжённый руководством по их использованию и (не всегда) изложением общей теории^[20]. Сравнение зиджей периода VIII—XIII веков показывает быструю эволюцию тригонометрических знаний. Самые ранние из сохранившихся трудов принадлежат ал-Хорезми и ал-Марвази (IX век), которые рассмотрели, наряду с известными ещё индийцам синусом и косинусом, новые тригонометрические функции: тангенс, котангенс, секанс и косеканс^[17].

Сабит ибн Курра (IX век) и ал-Баттани (X век) первыми открыли фундаментальную теорему синусов для частного случая прямоугольного сферического треугольника. Для произвольного сферического треугольника доказательство было найдено (разными способами и, вероятно, независимо друг от друга) Абу-л-Вафой, ал-Худжанди и ибн Ираком в конце X века^[13]. В другом трактате ибн Ирака сформулирована и доказана теорема синусов для плоского треугольника^[21]. Сферическая теорема косинусов в общем виде сформулирована в странах ислама не была, однако в трудах Сабита ибн Курры, ал-Баттани и других астрономов имеются эквивалентные ей утверждения^[22].

Фундаментальное изложение тригонометрии как самостоятельной науки (как плоской, так и сферической) дал персидский математик и астроном Насир ад-Дин ат-Туси в 1260 году^[23]. Его «Трактат о полном четырёхстороннике» содержит практические способы решения типичных задач, в том числе труднейших, решенных самим ат-Туси — например, построение сторон сферического треугольника по заданным трём углам^[24]. Таким образом, к концу XIII века были открыты базовые теоремы, необходимые для эффективного решения треугольников.

В Европе развитие тригонометрической теории стало чрезвычайно важным в Новое время, в первую очередь для артиллерии, оптики и навигации при дальних морских путешествиях. В 1551 году появились 15-значные тригонометрические таблицы Ретика, ученика Коперника, с шагом 10"^[25]. Потребность в сложных тригонометрических расчётах вызвала в начале XVII века открытие логарифмов, причём первые логарифмические таблицы Джона Непера содержали только логарифмы тригонометрических функций. Среди других открытий Непера — эффективный алгоритм решения сферических треугольников, получивший название «формулы аналогии Непера»^[26]. Алгебраизация тригонометрии, начатая Франсуа Виетом, была завершена Леонардом Эйлером в XVIII веке, после чего алгоритмы решения треугольников приобрели современный вид.

См. также

• История тригонометрии
• Сферическая тригонометрия
• Сферический треугольник
• Триангуляция
• Тригонометрические тождества
• Тригонометрические функции
• Формулы Мольвейде

Литература

Теория и алгоритмы

• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
• Основные понятия сферической геометрии и тригонометрии // Энциклопедия элементарной математики (в 5 томах). — М.: Физматгиз, 1963. — Т. 4. — С. 518-557. — 568 с.
• Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948.

История

• Глейзер Г. И. История математики в школе. VII-VIII классы. Пособие для учителей. — М.: Просвещение, 1982. — С. 76-95. — 240 с.
• Глейзер Г. И. История математики в школе. IX-X классы. Пособие для учителей. — М.: Просвещение, 1983. — 352 с.
• История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука.
  • История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
  • Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
  • Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
• Матвиевская Г. П. Очерки истории тригонометрии: Древняя Греция. Средневековый Восток. Позднее Средневековье. — Изд. 2-е. — М.: Либроком, 2012. — 160 с. — (Физико-математическое наследие: математика (история математики)). — ISBN 978-5-397-02777-9
• Рыбников К. А. История математики в двух томах. — М.: Изд. МГУ, 1960. — Т. I.
• Сираждинов С. Х., Матвиевская Г. П. Абу Райхан Беруни и его математические труды. Пособие для учащихся. — М.: Просвещение, 1978. — 95 с. — (Люди науки).
• Цейтен Г. Г. История математики в древности и в средние века. — М.-Л.: ГТТИ, 1932. — 230 с.
• Цейтен Г. Г. История математики в XVI и XVII веках. — М.-Л.: ОНТИ, 1938. — 456 с.

Ссылки

• Онлайн-триангулятор.  (англ.) Укажите известные величины, а программа вычислит оставшиеся и начертит треугольник.

Примечания

1. ↑ ^{1 2} Выгодский М. Я., 1978, с. 266-268.
2. ↑ Solving Triangles. Maths is Fun. Проверено 23 июля 2012.
3. ↑ Solving SSS Triangles. Maths is Fun. Архивировано из первоисточника 30 сентября 2012. Проверено 23 июля 2012.
4. ↑ Solving SAS Triangles. Maths is Fun. Архивировано из первоисточника 30 сентября 2012. Проверено 24 июля 2012.
5. ↑ Solving SSA Triangles. Maths is Fun. Архивировано из первоисточника 30 сентября 2012. Проверено 24 Jule 2012).
6. ↑ Выгодский М. Я., 1978, с. 294.
7. ↑ Solving ASA Triangles. Maths is Fun. Архивировано из первоисточника 30 сентября 2012. Проверено 24 июля 2012.
8. ↑ Цейтен Г. Г., 1932, с. 223-224.
9. ↑ Цейтен Г. Г., 1938, с. 126-127.
10. ↑ van der Waerden, Bartel Leendert. Geometry and Algebra in Ancient Civilizations. — Springer, 1983. — ISBN 3-540-12159-5
11. ↑ Глейзер Г. И., 1982, с. 77.
12. ↑ Глейзер Г. И., 1982, с. 94-95.
13. ↑ ^{1 2} Матвиевская Г. П., 2012, с. 92-96.
14. ↑ Матвиевская Г. П., 2012, с. 25-27.
15. ↑ Матвиевская Г. П., 2012, с. 33-36.
16. ↑ Матвиевская Г. П., 2012, с. 40-44.
17. ↑ ^{1 2} Сираждинов С. Х., Матвиевская Г. П., 1978, с. 79.
18. ↑ История математики, том I, 1970, с. 199-201.
19. ↑ История математики в Средние века, 1961, с. 160.
20. ↑ Матвиевская Г. П., 2012, с. 51-55.
21. ↑ Матвиевская Г. П., 2012, с. 111.
22. ↑ Матвиевская Г. П., 2012, с. 96-98.
23. ↑ Туси Насирэддин. Трактат о полном четырёхстороннике. Баку, Изд. АН АзССР, 1952.
24. ↑ Рыбников К. А., 1960, с. 105.
25. ↑ История математики, том I, 1970, с. 320.
26. ↑ Степанов Н. Н. §42. Формулы «аналогии Непера» // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 87-90. — 154 с.