Формула конечных приращений

У этого термина существуют и другие значения, см. Теорема Лагранжа.

Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция $f$ непрерывна на отрезке $[a; b]$ и дифференцируема в интервале $(a;b)$, то найдётся такая точка $c\in (a;b)$, что

$\frac{f(b)-f(a)}{b-a}=f'(c)$.

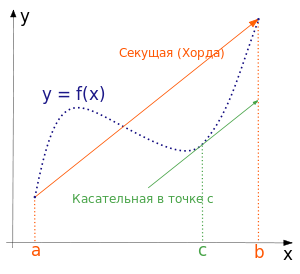
Геометрически это можно переформулировать так: на отрезке $[a;b]$ найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

Механическое истолкование: Пусть $f(t)$ — расстояние точки в момент $t$ от начального положения. Тогда $f(b)-f(a)$ есть путь, пройденный с момента $t=a$ до момента $t=b$, отношение $\frac{f(b)-f(a)}{b-a}$ — средняя скорость за этот промежуток. Значит, если скорость тела определена в любой момент времени $t\in (a,b)$, то в некоторый момент она будет равна своему среднему значению на этом участке.

Доказательство

Для функции одной переменной:

Введем функцию $F(x) = f(x)-\frac{f(b)-f(a)}{b-a}(x-a)$. Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны $f(a)$. Воспользовавшись упомянутой теоремой, получим, что существует точка $c$, в которой производная функции $F$ равна нулю:

$f'(c)-\frac{f(b)-f(a)}{b-a} = 0 \Leftrightarrow \frac{f(b)-f(a)}{b-a} = f'(c),$

что и требовалось доказать.

Следствия и обобщения

Теорема Лагранжа о конечных приращениях - одна из самых важных, узловая теорема во всей системе дифференциального исчисления. Она имеет массу приложений в вычислительной математике, и главнейшие теоремы математического анализа также являются её следствиями.

Следствие 1. Дифференцируемая на отрезке функция с производной, равной нулю, есть константа.

Доказательство. Для любых $x$ и $y$ существует точка $c$, такая что $f(y) - f(x) = f'(c) (y - x) = 0$. Значит, при всех $x$ и $y$ верно равенство $f(y) = f(x)$.

Следствие 2 (Формула Тейлора с остаточным членом в форме Лагранжа). Если функция $f$ дифференцируема $n$ раз в окрестности точки $x$, то для малых $h$ (т.е. тех, для которых отрезок $[x,x+h]$ лежит в указанной окрестности) справедлива формула Тейлора:

$f(x+h) = f(x) + f'(x)h + f''(x)\frac{h^2}{2} + ... + f^{(n-1)}(x)\frac{h^{n-1}}{(n-1)!} + f^{(n)}(x+\theta h)\frac{h^{n}}{n!}$

где $\theta$ - некоторое число из интервала $(0,1)$.

Замечание. Данное следствие является в то же время и обобщением. При $n=1$ из него получается сама теорема Лагранжа о конечных приращениях.

Следствие 3 (Формула Ньютона-Лейбница). Если функция $f(x)$ дифференцируема на отрезке $[a,b]$ и её производная интегрируема по Риману на этом отрезке, то справедлива формула: $\int\limits_{a}^{b}f'(x)dx = f(b) - f(a)$.

Доказательство. Пусть $T$ - произвольное разбиение $a=x_0 < x_1 < x_2 < ... <x_n = b$ отрезка $[a,b]$. Применяя теорему Лагранжа, на каждом из отрезков $[x_{k-1}, x_k]$ найдём точку $\xi_k$ такую, что $f'(\xi_k) (x_k - x_{k-1}) = f(x_k) - f(x_{k-1})$.

Суммируя эти равенства, получим: $\sum\limits_{k=1}^{n} f'(\xi_k) (x_k - x_{k-1}) = \sum\limits_{k=1}^{n} (f(x_k) - f(x_{k-1})) = f(b) - f(a)$

Cлева стоит интегральная сумма Римана для интеграла $\int\limits_{a}^{b}f'(x)dx$ и заданного отмеченного разбиения. Переходя к пределу по диаметру разбиения, получим формулу Ньютона-Лейбница.

Замечание. Следствием (и обобщением) формулы Ньютона-Лейбница является формула Стокса, а следствием формулы Стокса является интегральная теорема Коши - основная теорема теории аналитических функций (ТФКП).

Следствие 4 (Теорема об оценке конечных приращений). Пусть отображение $F:\Omega\rightarrow\mathbb{R}^m$ непрерывно дифференцируемо в выпуклой компактной области $\Omega$ пространства $\mathbb{R}^n$. Тогда $|F(y) - F(x)| \leq \sup\limits_{\xi\in \Omega}|DF(\xi)|\cdot |y - x|$.

Замечание. Без использования теоремы об оценке конечных приращений не обходятся доказательства таких теорем, как теорема об обратном отображении, теорема о неявной функции, теорема о существовании и единственности решения задачи Коши для обыкновенных дифференциальных уравнений.

См. также

• Лагранж, Жозеф Луи
• Теорема Коши — расширенный вариант этой теоремы.