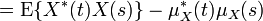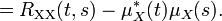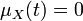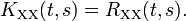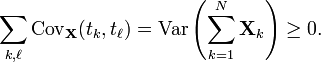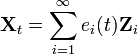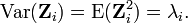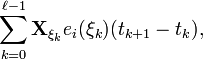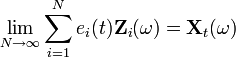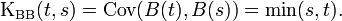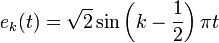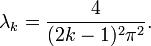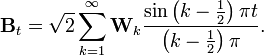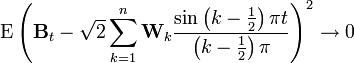- Теорема Кархунена-Лоэва
-
Теорема Кархунена-Лоэва
В теории стохастических процессов , теорема Карунена-Лоэва (названа в честь Кари Карунена и М.Лоэва)) — представление стохастического процесса, как бесконечной линейной комбинации ортогональных функций, аналогичного представлению рядов Фурье- последовательному представлению функций на ограниченном интервале. В отличие от рядов Фурье, где коэффициенты являются действительными числами и базис представления состоит из синусоидальных функций (то есть, из функций синус и косинус с разными частотами), коэффициенты в теореме Кархунена-Лоэва -случайные переменные, и базис представления зависит от процесса. Ортогональные базисные функции, использованные в этом представлении, определяет функция ковариации процесса. Если мы рассматриваем стохастический процесс как случайную функцию F, то есть процесс, в котором функция на интервале [a, b] принимает значение F, то эта теорема может рассматриваться как случайное ортонормальное расширение F.
В случае, если центрированный стохастический процесс {Xt}t ∈ [a, b] (где центрирование означает, что математические ожидания E(Xt) определены и равны 0, для всех значений параметра t на [a, b]), удовлетворяя техническому условию непрерывности, допускает разложение.
где Zk- взаимнонекоррелированые случайные переменные и функции ek- непрерывные вещественные функции, на [a, b], которые попарно ортогональны в метрике L² [a, b]. Общий случай нецентрированного процесса, может быть показан разложением функции математического ожидания в базисе ek.
Кроме того, если этот процесс гауссовский, то случайные величины Zk-тоже гауссовские и являются стохастически независимыми. Этот результат обобщает преобразования Карунена-Лоэва. Важным примером центрированного стохастического процесса на интервале [0,1], является винеровский процесс, и теорема Карунена-Лоэва может быть использована для получения канонического ортогонального представления. В этом случае расширение состоит из синусоидальных функций.
Приведенные выше разложения в также известны как разложения или декомпозиция Карунена-Лоэва (эмпирическая версия, то есть, с коэффициентами из исходных числовых данных), как анализ главных компонент, собственное ортогональное разложение или преобразование Хотеллинга.
Содержание
Формулировка
Сформулируем результат в терминах комплексно-значных стохастических процессов. Результаты могут быть приминимы к вещественнозначным процессам без модификаций, вспоминая, что комплексно-сопряженное действительное число- это то же самое число.
Если X и Y — случайные переменные, то внутренне произведение (скалярное) определяется формулой
где * обозначает операцию комплексного сопряжения.
Статистики второго порядка
Скалярное произведение определяется если как X, так и Y имеют ограниченные вторые моменты, эквивалентны, и если они оба квадратично интегрируемы. Отметим, что скалярное произведение связано с ковариацией и корреляцией. В частности, для случайных переменных со средним нулевым значением, ковариация и скалярное произведение совпадают. Функция автоковариации KXX
Если {Xt}t является центрируемым процессом, тогда
для всех t. Таким образом, автоковариация KXX равна автокорреляции RXX:
Отметим, что если {Xt}t центрируется и t1, ≤ t2, …, ≤ tN являются точками на интервале [a, b], следовательно
Формулировка теоремы
Теорема. Рассмотрим центрированный стохастический процесс {Xt}t, индексированный t на интервале [a, b] с функцией ковариации CovX. Предположим, что функция ковариации CovX(t,s) совместно непрерывна по t, s. Тогда CovX — позитивно определенное ядро, и по теореме Мерсера интегральный оператор T в L²[a,b] (близкой к мере Лебега на [a,b]) имеет ортонормированный базис из собственных векторов . Пусть {ei}i являются собственными векторами T, соответствующими ненулевым собственным значениям и
Тогда Zi — центрированные ортогональные случайные переменные и
где сходимость обеспечивается в среднем и является равномерной по t. Кроме того
где λi собственное значение соответствует собственному вектору ei.
Суммы Коши
В формулировке теоремы интеграл определения Zi может быть задан, как предел в среднем сумм Коши случайных переменных
Где
Особый случай: распределение Гаусса
Так как предел в среднем из совместно Гауссовых случайных переменных является совместно Гауссовым и совместно Гауссовые случайные (центрированные) переменные независимы и только, если они являются ортогональными, мы можем также заключить:
Теорема. Переменные Zi имеют совместное распределение Гаусса, и являются стохастически независимыми, если первоначальный процесс {Xt}t -тоже является Гауссовым.
В Гауссовом случае, поскольку переменные Zi являются независимыми, мы можем быть уверены в том, что:
почти очевидно.
Отметим, что обобщая теорему Мерсера, мы можем заменить интервал [a, b] другими компактными пространствами C , а меру Лебега на [a, b] — мерой Бореля, поддерживаемую на C.
Процесс Винера
Винеровский процесс в теории случайных процессов — это математическая модель броуновского движения или случайного блуждания с непрерывным временем. Здесь мы рассматриваем его в качестве центрируемого стандартного гауссовского процесса B(t) с ковариационной функцией
Собственные векторы ядра ковариации легко определяются:
так же, как и соответствующие собственные значения
Это позволяет получить нам следующее представление винеровского процесса :
Теорема. Существует последовательность {Wi}i из случайных гауссовых независимых переменных с средним равным 0 и дисперсией (вариацией), такая, что
Сходимость является равномерной по t в норме L² так, что
равномерно по t.
Использование
Было высказано мнение, что в проекте SETI, следует использовать преобразования Кархунена-Лоэва для обнаружения сигналов с очень широким спектром. Аналогично, в системах адаптивной оптики иногда используют функции Карунена-Лоэва для восстановления информации о фазе фронта волны. (Dai 1996, JOSA A).
См. также
Ссылки
- И. И. Гихман, А. В. Скороход, Введение в теорию случайных процессов.- М.: Наука, 1965.
- B. Simon, Functional Integration and Quantum Physics, Academic Press, 1979
- K. Karhunen, Kari, Uber lineare Methoden in der Wahrscheinlichkeitsrechnung, Ann. Acad. Sci. Fennicae. Ser. A. I. Math.-Phys., 1947, No. 37, 1-79
- М. Лоев, Теория вероятностей, — М.: ИЛ, 1962.
- G. Dai, Modal wave-front reconstruction with Zernike polynomials and Karhunen-Loeve functions, JOSA A, 13, 6, 1996
Wikimedia Foundation. 2010.
Метод главных компонент — (англ. Principal component analysis, PCA) один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих областях,… … Википедия

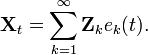
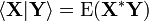
![K_\mathrm{XX}(t,s) = \operatorname{Cov}[ X(t),X(s) ] = \langle \mathbf{X}_t | \mathbf{X}_s \rangle](http://dic.academic.ru/pictures/wiki/files/98/b456d5e40408e574ee715cbd9cd53765.png)
![= \mathrm{E} \{ [ X(t)-\mu_X(t) ]^* [ X(s)-\mu_X(s) ] \} \,](http://dic.academic.ru/pictures/wiki/files/99/c44f75fe7d106db68f7da11f4afb995a.png)