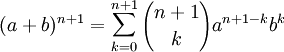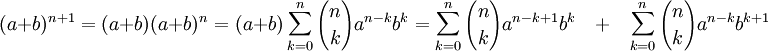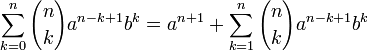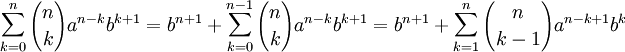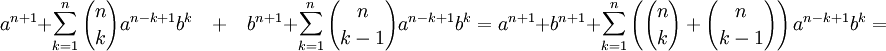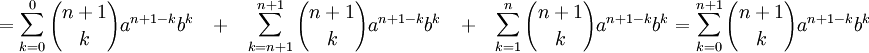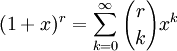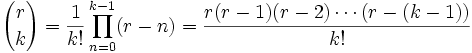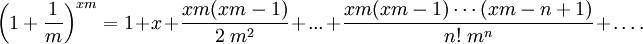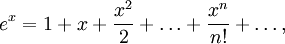Ньютона бином

Бином Ньютона — это формула

$(a+b)^n = {n\choose 0}a^n + {n\choose 1}a^{n-1}b + \dots + {n\choose k}a^{n-k}b^k + \dots + {n\choose n}b^n$,

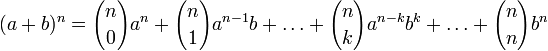где 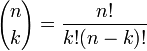${n\choose k}=\frac{n!}{k!(n-k)!}$ — биномиальные коэффициенты, n — неотрицательное целое число.

Доказательство

$(a+b)^n = \sum_{k=0}^n {n \choose k } a ^ {n-k} b ^ {k}$

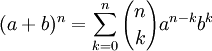
Докажем это равенство, используя метод математической индукции:

База индукции: n = 1

(a + b)¹ = a + b

Шаг индукции:

Пусть утверждение для n верно:

$(a+b)^n = \sum_{k=0}^n {n \choose k } a ^ {n-k} b ^ {k}$

Тогда надо доказать утверждение для n + 1:

$(a+b)^{n+1} = \sum_{k=0}^{n+1} {{n+1} \choose k } a ^ {n+1-k} b ^ {k}$

Начнём доказательство:

$(a+b)^{n+1} = (a+b)(a+b)^n=(a+b)\sum_{k=0}^{n} {n \choose k} a ^ {n-k} b ^ {k} = \sum_{k=0}^n {n \choose k} {a ^ {n - k + 1} b ^ {k}}\quad + \quad \sum_{k=0}^n {n \choose k} a ^ {n-k} b ^ {k+1}$

Извлечём из первой суммы слагаемое при k = 0

$\sum_{k=0}^n {n \choose k} {a ^ {n - k + 1} b ^ {k}} = a^{n+1} + \sum_{k = 1}^n {n \choose k} a ^ {n - k + 1} b ^ k$

Извлечём из второй суммы слагаемое при k = n

$\sum_{k=0}^n {n \choose k} a ^ {n-k} b ^ {k+1} = b^{n+1} + \sum_{k=0}^{n-1}{n \choose k}a^{n - k} b ^ {k+1} = b^{n+1} + \sum_{k = 1}^n {n \choose {k-1}} a^{n - k + 1} b ^ {k}$

Теперь сложим преобразованные суммы:

$a^{n+1} + \sum_{k = 1}^n {n \choose k} a ^ {n - k + 1} b ^ k \quad + \quad b^{n+1} + \sum_{k = 1}^n {n \choose {k-1}} a^{n - k + 1} b ^ {k} = a ^ {n + 1} + b ^ {n + 1} + \sum_{k = 1}^n \left( {n \choose k} + {n \choose {k - 1} } \right) a ^ {n - k + 1} b ^ k =$

$=\sum_{k=0}^0 {n+1 \choose k} a ^ {n + 1 - k} b ^ k \quad + \quad \sum_{k = n + 1}^{n+1} {n+1 \choose k} a^{n + 1- k}b^k \quad + \quad \sum_{k = 1} ^ {n} {n+1 \choose k} a ^ {n + 1 - k} b ^ k= \sum_{k=0}^{n+1} {{n+1} \choose k } a ^ {n+1-k} b ^ {k}$

Что и требовалось доказать

Комментарий:

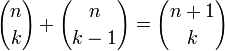${n \choose k} + {n \choose k - 1} = {n + 1 \choose k}$ — одно из тождеств биномиальных коэффициентов

Для ненатуральных степеней

$(1+x)^r=\sum_{k=0}^{\infty} {r \choose k} x^k$

где r может быть комплексным числом (в частности, отрицательным или вещественным). Коэффициенты находятся по формуле:

${r \choose k}={1 \over k!}\prod_{n=0}^{k-1}(r-n)=\frac{r(r-1)(r-2)\cdots(r-(k-1))}{k!}\,$

При этом ряд

$(1+z)^\alpha=1+\alpha{}z+\frac{\alpha(\alpha-1)}{2}z^2+...+\frac{\alpha(\alpha-1)\cdots(\alpha-n+1)}{n!}z^n+...$.

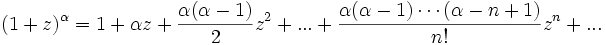сходится при $|z|\le 1$.

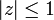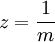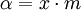В частности, при $z=\frac{1}{m}$ и $\alpha=x\cdot m$ получается тождество

$\left(1+\frac{1}{m}\right)^{xm}=1+x+\frac{xm(xm-1)}{2\; m^2}+...+\frac{xm(xm-1)\cdots(xm-n+1)}{n!\; m^n}+\dots.$

Переходя к пределу при 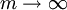$m\to\infty$ и используя второй замечательный предел 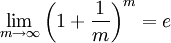$\lim_{m\to\infty}{\left(1+\frac{1}{m}\right)^{m}}=e$, выводим тождество

$e^x=1+x+\frac{x^2}{2}+\dots+\frac{x^n}{n!}+\dots,$

именно таким образом впервые полученное Эйлером.

История

Считается, что эту формулу, как и треугольник, позволяющий находить коэффициенты, изобрёл Блез Паскаль, описавший её в XVII веке. Тем не менее, она была известна ещё китайскому математику Яну Хуэю, жившему в XIII веке. Возможно, её открыл персидский учёный, поэт и философ Омар Хайям.

Исаак Ньютон обобщил формулу для прочих показателей степени.

В художественной литературе

В художественной литературе «бином Ньютона» появляется в нескольких запоминающихся контекстах, где речь идёт о чём-либо сложном.

• В рассказе А. Конан Дойля «Последнее дело Холмса» Холмс говорит о математике профессоре Мориарти:

«Когда ему исполнился двадцать один год, он написал трактат о биноме Ньютона, завоевавший ему европейскую известность. После этого он получил кафедру математики в одном из наших провинциальных университетов, и, по всей вероятности, его ожидала блестящая будущность».

• Знаменита цитата из «Мастера и Маргариты» М. А. Булгакова: «Подумаешь, бином Ньютона!».

Об этой специфической роли бинома Ньютона в культуре писал известный математик В. А. Успенский [1].

См. также

• Формулы сокращённого умножения многочленов — наиболее частые частные случаи бинома Ньютона
• Биномиальное распределение