- ГАЗОВОЙ ДИНАМИКИ УРАВНЕНИЯ
- математическое выражение основных законов сохранения массы, импульса, энергии газа, описывающих состояние газа. Газ есть совокупность большого числа частиц (молекул, атомов, ионов), находящихся в непрерывном хаотич. движении. Учет взаимодействия и движения каждой частицы газа является чрезвычайно трудной проблемой, поэтому для описания состояния газа применяют статистический или континуальный подход. При таком подходе состояние ансамбля частиц газа характеризуется функцией распределения частиц, определенной или в 7-мерном фазовом пространстве
 или 4-мерном пространстве
или 4-мерном пространстве  В первом случае рассматривается скалярная функция распределения
В первом случае рассматривается скалярная функция распределения

в к-рой величины
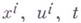 - непрерывно меняющиеся аргументы,
- непрерывно меняющиеся аргументы, и
и  меняются в конечных или бесконечных интервалах,
меняются в конечных или бесконечных интервалах,  Сама функция
Сама функция  удовлетворяет интегро-дифференциальному уравнению Больцмана (см. Больцмана уравнение, Кинетическое уравнение).или же, в зависимости от физич. предпосылок, другим уравнениям (см. Боголюбова цепочка уравнений, Власова кинетическое уравнение). Во втором случае функция распределения, описывающая состояние газа, является векторной функцией
удовлетворяет интегро-дифференциальному уравнению Больцмана (см. Больцмана уравнение, Кинетическое уравнение).или же, в зависимости от физич. предпосылок, другим уравнениям (см. Боголюбова цепочка уравнений, Власова кинетическое уравнение). Во втором случае функция распределения, описывающая состояние газа, является векторной функцией

зависящей от четырех аргументов
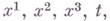 непрерывно и независимо меняющихся в интервалах
непрерывно и независимо меняющихся в интервалах 
 В этом случае под частицей, строго говоря, следует понимать материальный элемент газа, занимающий бесконечно малый объем и обладающий определенной скоростью
В этом случае под частицей, строго говоря, следует понимать материальный элемент газа, занимающий бесконечно малый объем и обладающий определенной скоростью  к-рая является функцией аргументов
к-рая является функцией аргументов  Здесь
Здесь 
 -плотность газа, т. е. масса газа, приходящаяся на единицу объема,
-плотность газа, т. е. масса газа, приходящаяся на единицу объема, 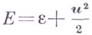 - полная энергия единицы массы газа,
- полная энергия единицы массы газа,  - внутренняя энергия единицы массы газа.
- внутренняя энергия единицы массы газа.
В предположении локального термодинамич. равновесия из уравнений Больцмана следуют законы сохранения газовой динамики в интегральной форме. В инер-циальной ортонормированной системе координат:

где
 - объем пространства, ограниченный поверхностью
- объем пространства, ограниченный поверхностью 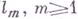 . Соотношения (1) справедливы для произвольного объема
. Соотношения (1) справедливы для произвольного объема  с границей
с границей  -мерном фазовом пространстве
-мерном фазовом пространстве  . Величины
. Величины  в трехмерном случае имеют следующий вид:
в трехмерном случае имеют следующий вид:
 (2)
(2)

 - давление газа,
- давление газа,  - температура газа,
- температура газа,  - символ Кронекера,
- символ Кронекера, - коэффициент вязкости сжатия,
- коэффициент вязкости сжатия,  - коэффициент вязкости сдвига,
- коэффициент вязкости сдвига,  - коэффициент теплопроводности. При записи формул употребляются правила записи формул тензорного анализа.
- коэффициент теплопроводности. При записи формул употребляются правила записи формул тензорного анализа.
Для гладких течений получается система дифференциальных уравнений в дивергентной форме:
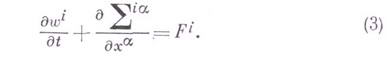
Эта система уравнений становится замкнутой после присоединения уравнений состояния. В случае термодина-мич. равновесия уравнения состояния принимают вид:

В неравновесном случае эти величины могут зависеть от градиентов функции течения.
Представление (2) имеет определенный физич. смысл:
 соответствует конвективным потокам массы, импульса, энергии,
соответствует конвективным потокам массы, импульса, энергии,  - шаровой недиссипативной части тензора напряжений, т. е. давлению,
- шаровой недиссипативной части тензора напряжений, т. е. давлению,  - диссипативной части напряжений (вязкость, диффузия тепла) и используется в методе расщепления для получения эффективных схем интегрирования задач газовой динамики.
- диссипативной части напряжений (вязкость, диффузия тепла) и используется в методе расщепления для получения эффективных схем интегрирования задач газовой динамики.
Для описания течения газа могут применяться различные системы координат. Кроме системы координат, неподвижно связанной с физич. пространством и являющейся галилеевой (эйлерова система координат), применяются различные подвижные, не обязательно декартовы и галилеевы системы координат. Очень распространенной является лагранжева система координат, связанная с частицами газа. В этой системе координат каждый материальный элемент имеет фиксированную координату. Эйлеров способ состоит в том, что в каждый момент времени tпараметры состояния газа определяются как функции координат
 (эйлеровы координаты) точки в нек-рой неподвижной системе координат и вектор
(эйлеровы координаты) точки в нек-рой неподвижной системе координат и вектор 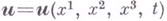 означает скорость частицы газа, находящейся в момент времени tв точке
означает скорость частицы газа, находящейся в момент времени tв точке  Способ Лагранжа предполагает задание скорости ии термодинамич. величин для каждой частицы как функций времени t. Зафиксировав частицу газа с помощью параметров
Способ Лагранжа предполагает задание скорости ии термодинамич. величин для каждой частицы как функций времени t. Зафиксировав частицу газа с помощью параметров  получают параметры течения газа как функции от времени
получают параметры течения газа как функции от времени  (лаг-ранжевы координаты). Связь между эйлеровыми и лагранжевыми координатами имеет вид:
(лаг-ранжевы координаты). Связь между эйлеровыми и лагранжевыми координатами имеет вид:

где
 - эйлеровы координаты частицы, находившейся в момент времени t=0 в точке
- эйлеровы координаты частицы, находившейся в момент времени t=0 в точке  В случае одной пространственной переменной при условии, что газодинамич. переменные являются непрерывно дифференцируемыми функциями, уравнения вязкого теплопроводного газа имеют вид: в эйлеровых координатах
В случае одной пространственной переменной при условии, что газодинамич. переменные являются непрерывно дифференцируемыми функциями, уравнения вязкого теплопроводного газа имеют вид: в эйлеровых координатах

в лагранжевых координатах

где

Для произвольной подвижной системы координат во многих случаях целесообразно одновременно преобразовывать компоненты скорости по тензорному закону. Если

есть преобразование пространственных координат, при к-ром временная координата не изменяется, то отображение (5) можно связать с самим течением газа и тогда оно будет определять поле локальных систем координат, зависящих от самого течения. Возможны и более общие преобразования, включающие изменение временной координаты.
Большую роль в теории Г. д. у. и в приложениях играет анализ малых параметров
 (
( - коэффициент сжимаемости), входящих в уравнения (3). Если
- коэффициент сжимаемости), входящих в уравнения (3). Если  , то (3) - уравнения идеальной газовой динамики; если
, то (3) - уравнения идеальной газовой динамики; если  то (3) - уравнения Навье - Стокса несжимаемой жидкости. Эти уравнения не принадлежат к типу Коши - Ковалевской. В случае
то (3) - уравнения Навье - Стокса несжимаемой жидкости. Эти уравнения не принадлежат к типу Коши - Ковалевской. В случае  получается система уравнений типа Коши - Ковалевской параболич. типа, не являющаяся сильно параболической. В теории турбулентности и неньютоновых жидкостей коэффициенты
получается система уравнений типа Коши - Ковалевской параболич. типа, не являющаяся сильно параболической. В теории турбулентности и неньютоновых жидкостей коэффициенты  могут зависеть от градиентов газодинамич. величин.
могут зависеть от градиентов газодинамич. величин.
Определяющие соотношения (2) и, в частности, уравнения состояния (4) характеризуют тип системы Г. д. у. (3) и ряд ее качественных особенностей. Так, в случае идеального сжимаемого газа
 система уравнений (3) является гиперболической, если
система уравнений (3) является гиперболической, если

где энтропия Sопределяется соотношением (второй закон термодинамики)

Условие (6) является локальным, зависит от решения и в нек-рых случаях может нарушаться. Так, в случае уравнения состояния Ван-дер-Ваальса условие (6) может нарушаться, уравнения становятся эллиптическими, решение - неустойчивым.
Законы сохранения (1) позволяют сформулировать обобщенное решение Г. д. у., к-рое уже не обязательно является непрерывным и не удовлетворяет дифференциальным Г. д. у. (3). Полная теория обобщенных решений Г. д. у. не создана, однако хорошо изучены простейшие обобщенные решения, как, напр., ударная волна, центрированная волна разрежения, контактное течение и т. д. Существует гипотеза, согласно к-рой обобщенное решение уравнений идеального сжимаемого газа есть предел соответствующего решения вязкого газа при
 Это утверждение строго доказано для одномерных ударных волн и в нек-рых частных случаях для уравнений типа
Это утверждение строго доказано для одномерных ударных волн и в нек-рых частных случаях для уравнений типа

Особый интерес представляют собой стационарные Г. д. у., к-рые в основном связаны с задачами стационарного обтекания тел в бесконечном пространстве или стационарных течений в каналах. В этом случае решение системы уравнений (3) не зависит от t, и система принимает вид:

Для стационарной системы уравнений (7) ставится нек-рая краевая задача, к-рая может быть весьма сложной, а само уравнение (7) может быть как эллиптического, так и смешанного типов. Напр., для задачи обтекания идеального сжимаемого газа в предположении потенциальности течения получается следующее уравнение в двумерном случае:

где
 - потенциал скорости, квадрат скорости звука
- потенциал скорости, квадрат скорости звука  может быть определен из интеграла Бернулли:
может быть определен из интеграла Бернулли:

Для уравнения (8) может быть поставлена задача обтекания данного контура l:

где un- нормальная составляющая вектора скорости по нормали к контуру l. В случае
 уравнение (8) имеет гиперболич. тип, в случае
уравнение (8) имеет гиперболич. тип, в случае 
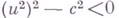 - эллиптич. тип. Возможен переход от эллиптич. типа к гиперболическому (трансзвуковой поток). Можно показать, что краевая задача в случае трансзвукового обтекания является некорректной, так как сколь угодно малое изменение контура может сделать краевую задачу неразрешимой в классе непрерывных функций.
- эллиптич. тип. Возможен переход от эллиптич. типа к гиперболическому (трансзвуковой поток). Можно показать, что краевая задача в случае трансзвукового обтекания является некорректной, так как сколь угодно малое изменение контура может сделать краевую задачу неразрешимой в классе непрерывных функций.
Большой интерес представляют задачи газодинамич. неустойчивости и турбулентности, к-рые описываются, как правило, в рамках теории несамосопряженных уравнений (уравнение Орра-Зоммерфельда, уравнение Рейнольдса). В связи с практич. приложениями приобрели большое значение Г. д. у., описывающие движение более сложных сред (многофазные среды, неньютоновы жидкости, магнитная гидродинамика). Большинство уравнений математич. физики представляют собой результат линеаризации Г. д. у.
О численном решении задач газовой динамики см. ст. Газовой динамики численные методы.
Лит.:[1] Серрин Дж., Математические основы классической механики жидкости, пер. с англ., М., 1963; [2] Седов Л. И., Механика сплошной среды, т. 1-2, М., 1970; [3] Ландау Л. Д., Лифшиц Е. М., Механика сплошных сред, 2 изд., М., 1954; [4] Кочин Н. Е., Кибель И. А., Розе Н. В., Теоретическая гидромеханика, ч. 1-2, М., 1963; [5] Брановер Г. Г., Цинобер А. М., Магнитная гидродинамика несжимаемых сред, М., 1970; [6] Рождественский В. Л., Яненко Н. Н., Системы квазилинейных уравнений и их приложения к газовой динамике, М., 1968.
Ю. И. Шокин, Н. Н. Яненко.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
