ВЕЙЕРШТРАССА

ВЕЙЕРШТРАССА

-ФУНКЦИЯ в классическом вариационном исчислении- функция, выделяющая главную часть приращения функционала при варьировании экстремали при помощи локальной (игольчатой) вариации с заданным значением ее производной в фиксированной точке экстремали. Для функционала


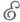-функция имеет вид


Если ввести функцию


(см. Лежандра преобразование, Понтрягина принцип максимума), то 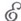-функция принимает вид


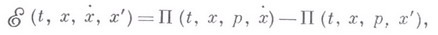
где Общая конструкция, приводящая к функциям, аналогичным 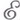-функции (1), состоит в следующем. Пусть 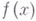- дифференцируемая или выпуклая функция, заданная в банаховом пространстве - сопряженное пространство. Если функция определяется равенством


где - производная функции в точке 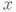(или элемент субдифференциала, если выпукла), то функция


есть -функция, построенная по . В случае, если дифференцируема,


т. е. -функция есть разность в точке между функцией f и линейной функцией, касательной к в 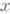. Сравнение формул (1) и (2) показывает, что 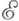-функция в классич. вариационном исчислении получается из конструкции (2) относительно переменных, связанных с производными, а переменные 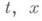играют роль параметров. Для случая функционала


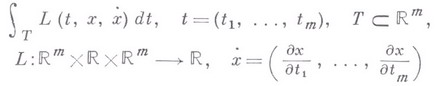
многомерной вариационной задачи -функция имеет вид


Для Лагранжа задачи с ограничениями и множителями Лагранжа -функция имеет вид (1), где 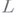заменяется на


-функция была впервые введена К. Вейерштрассом в 1879 (см. [1]) и лежит в основе теории-вариационного исчисления. В терминах -функции формулируются необходимое и (отдельно) достаточное условия экстремума (см. Вейерштрасса условия), через -функции выражается в виде конечного интеграла приращение функционала на экстремали (см. Вейерштрасса формула для приращения функционала).

Особенно важную роль в вариационном исчислении играют гладкие функционалы, у к-рых в нек-рой области параметров для всех или, сильнее, если для всех . . Они наз. к в а-з и регулярными (соответственно регулярными, или эллиптическими). Для них всегда выполнены Лежандра условие и необходимое Вейерштрасса условие, а также справедливы теоремы существования и регулярности [7].

Лит.:[1] Weierstrass К., Vorlesungen uber Varia-tionsrechnung (Math. Werke, Bd 7), Lpz., 1927; [2] Caratheodory C., Variationsrechnung und partielle Differentialgleichungen erster Ordiumg, B.-Lpz., 1935; [3] Воlza O., Vorlesungen uber Variationsrechnung, Lpz., 1949; [4] Ахиезер Н. И., Лекции по вариационному исчислению, М., 1955; [5] Понтрягин Л. С. [и др.], Математическая теория оптимальных процессов, 2 изд., М., 1969; [6] Hestenes M. R., Calculus of variations and optimal control theory, N. Y,-L., 1966; [7] Проблемы Гильберта, М", 1969; 18] Блисс Г., Лекции по вариационному исчислению, пер. с англ., М., 1950. В. М. Тихомиров.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужен реферат?

Полезное


Смотреть что такое "ВЕЙЕРШТРАССА" в других словарях:

  • ВЕЙЕРШТРАССА — ФУНКЦИЯ см. Вейерштрасса эллиптические функции …   Математическая энциклопедия

  • Вейерштрасса теорема — [Weierstrass theorem] фундаментальная теорема математического программирования, формулирующая условия существования глобального максимума (см. Максимизация). Заключается в том, что если допустимое множество X является компактным и непустым (см.… …   Экономико-математический словарь

  • Вейерштрасса теорема — Фундаментальная теорема математического программирования, формулирующая условия существования глобального максимума (см. Максимизация). Заключается в том, что если допустимое множество X является компактным и непустым (см. статью Множество), то… …   Справочник технического переводчика

  • ВЕЙЕРШТРАССА ТЕОРЕМА — 1) В. т. о бесконечном про и введении [1]: для любой наперед заданной последовательности точек плоскости комплексного переменного существует целая функция, имеющая нулями точки этой последовательности и только пх. Эта функция может быть построена …   Математическая энциклопедия

  • ВЕЙЕРШТРАССА УСЛОВИЯ — экстремума необходимое и (отдельно) достаточное условия сильного экстремума в классическом вариационном исчислении. Предложены К. Вейерштрассом (К. Weierstrass, 1879). Необходимое условие Вейерштрасса: для того чтобы функционал достигал… …   Математическая энциклопедия

  • ВЕЙЕРШТРАССА ФОРМУЛА — для приращения функционала формула классич. вариационного исчисления, задающая значения функционала в виде криволинейного интеграла от Вейерштрасса функции. Пусть вектор функция является экстремалью функционала и при этом она включена в поле… …   Математическая энциклопедия

  • ВЕЙЕРШТРАССА - ЭРДМАНА УГЛОВЫЕ УСЛОВИЯ — дополнительные к Эйлера уравнению необходимые условия экстремума, задаваемые в точках, где экстремаль имеет излом. Пусть функционал классического вариационного исчисления, а экстремаль . непрерывно дифференцируема в окрестности точки за… …   Математическая энциклопедия

  • ВЕЙЕРШТРАССА КОЛЬЦО — локальное гензелево псевдогеометрическое (см. Геометрическое кольцо).кольцо, каждое факторкольцо к рого по простому идеалу является конечным расширением регулярного локального кольца. В. к. аналитически неприводимо. Любое конечное расширение В. к …   Математическая энциклопедия

  • ВЕЙЕРШТРАССА КООРДИНАТЫ — одни из видов координат в эллиптическом пространстве. Пусть эллиптическое пространство, а иаометричное ему пространство, полученное отождествлением диаметрально противоположных точек единичной сферы мерного евклидова пространства. В. к. точкп… …   Математическая энциклопедия

  • ВЕЙЕРШТРАССА - СТОУНА ТЕОРЕМА — широкое обобщение классической Вейерштрасса теоремы о приближении функций, принадлежащее М. Стоуну (М. Stone, 1935). Пусть кольцо непрерывных функций на бикомпакте с топологией равномерной сходимости, порожденной нормой и пусть есть подкольцо,… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»