- ВАРИАЦИЯ ФУНКЦИИ
числовая характеристика функции одного действительного-переменного, связанная с ее дифференциальными свойствами.
1) Пусть
 - функция действительного переменного х, заданная на отрезке
- функция действительного переменного х, заданная на отрезке  ; ее вариация
; ее вариация  есть точная верхняя грань сумм вида
есть точная верхняя грань сумм вида

где
 - произвольная система точек из
- произвольная система точек из  . Это определение предложено К. Жорда-ном [1]. Если
. Это определение предложено К. Жорда-ном [1]. Если  , то говорят, что функция
, то говорят, что функция 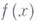 имеет ограниченную (конечную) вариацию на отрезке
имеет ограниченную (конечную) вариацию на отрезке  , а класс всех таких функций обозначают через
, а класс всех таких функций обозначают через  или просто через V. Функция
или просто через V. Функция 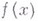 принадлежит классу
принадлежит классу  тогда и только тогда, когда она может быть представлена в виде
тогда и только тогда, когда она может быть представлена в виде 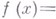
 где
где  и
и  - возрастающие (убывающие) на
- возрастающие (убывающие) на  функции (Жордана разложение функции ограниченной вариации). Сумма, разность и произведение двух функций класса
функции (Жордана разложение функции ограниченной вариации). Сумма, разность и произведение двух функций класса  также есть функция класса
также есть функция класса  . Это справедливо и для частного двух функций класса
. Это справедливо и для частного двух функций класса  , если модуль знаменателя превосходит положительную постоянную на отрезке
, если модуль знаменателя превосходит положительную постоянную на отрезке 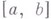 . Каждая функция класса
. Каждая функция класса  ограничена и может иметь не более чем счетное множество точек разрыва, причем все они 1-го рода.
ограничена и может иметь не более чем счетное множество точек разрыва, причем все они 1-го рода.
Все эти свойства функций класса
 установлены К. Жорданом [1] (см. также [2], с. 234-38).
установлены К. Жорданом [1] (см. также [2], с. 234-38).
Функции
 класса
класса 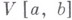 почти всюду дифференцируемы на
почти всюду дифференцируемы на  и для них имеет место разложение
и для них имеет место разложение

где
 - абсолютно непрерывная,
- абсолютно непрерывная,  - сингулярная функция, а
- сингулярная функция, а  - функция скачков (Лебега разложение фуикции ограниченной вариации). Это разложение единственно, если
- функция скачков (Лебега разложение фуикции ограниченной вариации). Это разложение единственно, если  (см. [3] и [2], с. 290).
(см. [3] и [2], с. 290).
Первоначально класс
 был введен К. Жорданом в связи с обобщением Дирихле признака сходимости рядов Фурье кусочно монотонных функций. К. Жор-дан доказал, что ряды Фурье
был введен К. Жорданом в связи с обобщением Дирихле признака сходимости рядов Фурье кусочно монотонных функций. К. Жор-дан доказал, что ряды Фурье  -периодич. функций класса
-периодич. функций класса  сходятся в каждой точке действительной оси. Однако в дальнейшем функции ограниченной вариации нашли широкое применение в различных областях математики, особенно в теории интеграла Стилтьеса.
сходятся в каждой точке действительной оси. Однако в дальнейшем функции ограниченной вариации нашли широкое применение в различных областях математики, особенно в теории интеграла Стилтьеса.
Иногда рассматриваются классы
 , к-рые определяются следующим образом. Пусть
, к-рые определяются следующим образом. Пусть 
 положительная при
положительная при  монотонно возрастающая непрерывная функция. Обозначим через
монотонно возрастающая непрерывная функция. Обозначим через  точную верхнюю грань сумм вида
точную верхнюю грань сумм вида
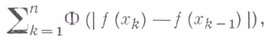
где
 - произвольное разбиение отрезка
- произвольное разбиение отрезка  . Величина
. Величина 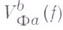 наз. Ф-вариацией функции
наз. Ф-вариацией функции  на отрезке
на отрезке  . Если
. Если  то говорят, что функция
то говорят, что функция  имеет ограниченную Ф - вариацию на отрезке
имеет ограниченную Ф - вариацию на отрезке  , а класс всех таких функций обозначается через
, а класс всех таких функций обозначается через 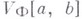 или просто через
или просто через  (см. (4], с. 287). При
(см. (4], с. 287). При  получается класс
получается класс  К. Жордана, а при
К. Жордана, а при 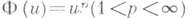 - классы Vp Н. Винера [5]. Определение класса V Ф[a, b] предложено Л. Юнг [6]. Если
- классы Vp Н. Винера [5]. Определение класса V Ф[a, b] предложено Л. Юнг [6]. Если

то

В частности,
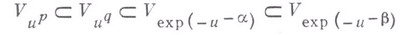
при
 причем эти вложения строгие.
причем эти вложения строгие.
Лит.: [1] Jоrdan С., "С. r. Acad. sci.", 1881, t. 92, № 5, p. 228-30; [2] Натансон И. П., Теория функций вещественной переменной, 2 изд., М., 1957; [З] Лебег А., Интегрирование и отыскание примитивных функций, (пер. с франц.), М.- Л., 1934; [4] Бари Н. К., Тригонометрические ряды, М., 1961; [5] Wiеner N., "Massachusetts J. Math, and Phys.", 1924, v. 3, p. 72-94; Г6] Young L. С., "C. r. Acad. sci.", 1937, t. 204, № 7, p. 470 - 72. Б. И. Голубое.
2) Для функции нескольких переменных имеются различные определения вариаций ( Арцела вариация, Витали вариация, Пьерпонта вариация, Тонелли плоская вариация, Фреше вариация, Хардп вариация). Очень плодотворным оказалось также следующее определение (см. [1]), основанное на использовании Банаха индикатрисы,. Пусть действительнозначная функция
 задана и измерима по Лебегу на n-мерном кубе
задана и измерима по Лебегу на n-мерном кубе 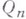 . Вариацией
. Вариацией  порядка
порядка 
 функции
функции 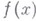 на кубе
на кубе  наз. число
наз. число

где
 обозначает
обозначает  -ю вариацию множества
-ю вариацию множества  , а интеграл понимается в смысле Лебега. Ото определение позволяет перенести на функции нескольких переменных многие свойства функций ограниченной вариации одного переменного. Напр.:
, а интеграл понимается в смысле Лебега. Ото определение позволяет перенести на функции нескольких переменных многие свойства функций ограниченной вариации одного переменного. Напр.:

б) Если последовательность функций
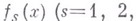
 сходится к
сходится к  равномерно на
равномерно на 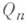 , то
, то

в) Если функция
 непрерывна на
непрерывна на  и все ее вариации конечны, то
и все ее вариации конечны, то  почти всюду имеет полный дифференциал.
почти всюду имеет полный дифференциал.
г) Если функция
 абсолютно непрерывна на
абсолютно непрерывна на  , то
, то
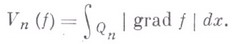
д) Если функция
 непрерывна на кубе
непрерывна на кубе  со стороной
со стороной  , имеет конечные вариации всех порядков на кубе
, имеет конечные вариации всех порядков на кубе  и может быть периодически продолжена с периодом
и может быть периодически продолжена с периодом 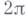 по каждому аргументу
по каждому аргументу  на все н-мерное пространство, то ее ряд Фурье равномерно сходится к ней на
на все н-мерное пространство, то ее ряд Фурье равномерно сходится к ней на  по Прингсхейму.
по Прингсхейму.
Достаточные условия конечности вариаций: если функция
 имеет на кубе
имеет на кубе  непрерывные производные всех порядков до
непрерывные производные всех порядков до  -го включительно, то ее вариация порядка kконечна. Эта теорема является окончательной в том смысле, что условия на гладкость не улучшаема ни прп одном k.
-го включительно, то ее вариация порядка kконечна. Эта теорема является окончательной в том смысле, что условия на гладкость не улучшаема ни прп одном k.
Лит.:[1] Витушкин А. Г., О многомерных вариациях, М., 1955 А. Г. Витушкин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
