- БИКАТЕГОРИЯ
- категория
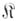 , в к-рой выделены подкатегория эпиморфизмов
, в к-рой выделены подкатегория эпиморфизмов 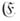 и подкатегория мономорфизмов
и подкатегория мономорфизмов 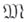 таким образом, что выполняются следующие условия:
таким образом, что выполняются следующие условия:
1) всякий морфизм
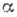 из категории
из категории 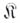 разлагается в произведение
разлагается в произведение 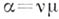 , где
, где 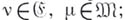
2) если
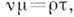 где
где 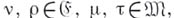 _ то существует такой изоморфизм
_ то существует такой изоморфизм 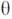 , что
, что 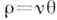 , и
, и 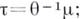
3)
 совпадает с классом изоморфизмов категории
совпадает с классом изоморфизмов категории 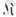 .
.
Эпиморфизмы из
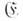 (мономорфизмы из
(мономорфизмы из 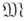 ) наз. допустимыми эпиморфизмами (мономорфизмам и) бикатегории.
) наз. допустимыми эпиморфизмами (мономорфизмам и) бикатегории.
Понятие Б. аксиоматизирует возможность разложения произвольного отображения в произведение сюръективного и инъективного отображений. Категория множеств, категория множеств с отмеченной точкой, категория групп являются бикатегориями с единственной бикатегорной структурой. В категории всех топо-логич. пространств, а также в категории всех ассоциативных колец имеется целый класс различных бикате-горных структур.
Лит.:[1] Цаленко М. Ш., Шульгейфер Е. Г., Основы теории категорий, М., 1974. М. Ш. Цаленко.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
