ПСЕВДОГРУППА

преобразований дифференцируемого многообразия М - семейство диффеоморфизмов открытых подмножеств многообразия Мв М, замкнутое относительно композиции отображений, перехода к обратному отображению, а также сужения и склейки отображений. Точнее, псевдогруппа преобразований (п. п.) Г многообразия Мсостоит из локальных преобразований, т. е. пар вида , где D_p - открытое подмножество в М, а - диффеоморфизм , причем предполагается, что 1) 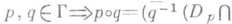2) , 3) , 4) если - диффеоморфизм открытого подмножества 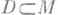в М и , где D_a - открытые подмножества в М, то 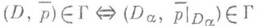для любого a. Видоизменяя должным образом условия 1)-4), можно определить п. п. произвольного топологич. пространства (см. [7]) или даже произвольного множества. Так же, как группа преобразований, п. п. определяет на Мотношение эквивалентности; классы эквивалентности наз. ее орбитами. П. п. Г многообразия Мназ. транзитивной, если М- ее единственная орбита, и наз. примитивной, если в Мнет нетривиальных гладких Г-инвариантных слоений (в противном случае п. п. наз. и м примитивной).

П. п. Г дифференцируемого многообразия Мназ. п. п. Ли, определяемой системой Sдифференциальных уравнений в частных производных, если Г состоит из тех и только тех локальных преобразований многообразия М, к-рые удовлетворяют системе S. Напр., П. конформных преобразований плоскости - это п. п. Ли, определяемая уравнениями Коши - Римана. Порядком п. п. Ли наз. минимальный порядок определяющей ее системы дифференциальных уравнений.

Примеры п. п. Ли. 1) П. всех голоморфных локальных преобразований n-мерного комплексного пространства . 2) П. всех голоморфных локальных преобразований пространства с постоянным якобианом.

3) П. всех голоморфных локальных преобразований пространства с якобианом, равным 1.

4) Гамильтонова псевдогруппа, состоящая из всех голоморфных локальных преобразований пространства (пчетно), сохраняющих дифференциальную 2-форму

5) П. всех голоморфных локальных преобразований пространства , сохраняющих форму w с точностью до постоянного множителя. 6) Контактная псевдогруппа, состоящая из всех голоморфных локальных преобразований пространства (при ), сохраняющих с точностью до (функционального) множителя дифференциальную 1-форму

7) Вещественные аналоги комплексных п. п. из примеров 1) - б). Порядки п. п. Ли из примеров 1), 3) - 6) равны 1, а в примере 2) порядок равен 2.

Любая группа Ли Gпреобразований многообразия Мопределяет п. п. Г(G), состоящую из ограничений преобразований из Gна открытые подмножества многообразия М. П. п. вида Г(G) наз. глобализуемыми. Так, П. локальных конформных преобразований сферы Sⁿ глобализуема при n>2 и не глобализуема при n=2.

П. п. Ли Г наз. п. п. конечного типа, если найдется такое натуральное число d, что любое локальное преобразование однозначно определяется своей d-струей в нек-рой точке ; наименьшее такое число dназ. степенью, или типом, п. п. Г; если же такого dне существует, то Г наз, д. п. бесконечного типа, П. п. в примерах 1) - 6) - примитивные п. п. Ли бесконечного типа.

Пусть Г - транзитивная п. п. Ли n-мерного дифференцируемого многообразия Ми G^r (Г) - совокупность всех r-струй локальных преобразований из Г, сохраняющих точку , т. е. таких , что и . Множество G^r (Г), снабженное естественной структурой группы Ли, наз. группой изотропии r-го порядкап. п. Г (группа G¹ (Г) наз. также линейной группой изотропии п. п. Г). Алгебра Ли группы G^r (Г) естественным образом вкладывается в алгебру Ли r-струй векторных полей на Мв точке О, Если Г - п. п. Ли первого порядка, то ядро G^(r) (Г).естественного гомоморфизма при любом зависит только от линейной группы изотропии G¹ (Г) и наз. ее r-м продолжением. П. ц. Ли Г первого порядка тогда и только тогда явдяется п. п. конечного типа d, когда

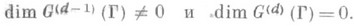
Если при этом линейная группа изотропии G¹ (Г) неприводима, то (см. [5]). Для того чтобы п. п. Ли Г первого порядка была п. п. конечного типа, необходимо, а в комплексном случае и достаточно, чтобы алгебра Ли не содержала эндоморфизмов ранга 1 (см. [10]). Такие линейные алгебры Ли наз. эллиптическими.

Для п. п. Ли Г первого порядка в терминах ее линейной алгебры изотропии вычислены алгебры Ли всех продолжений G^(r) (Г),. А именно, алгебра Ли группы G^(r) (Г) состоит из (r+1)-струй векторных полей на Мв точке О, имеющих в нек-рой локальной системе координат (x¹, х ², . . ., х ^п).вид

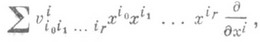
где - произвольный тензор, симметричный по нижним индексам и удовлетворяющий условию: при любых фиксированных i₁, i₂, . . ., i_r матрица

содержится в алгебре Ли , отнесенной к системе координат ( х ⁱ).

Пусть М - n -мерное дифференцируемое многообразие над нолем 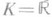или . Всякая транзитивная п. п. Ли Г порядка kмногообразия Мсовпадает с П. всех локальных автоморфизмов нек-рой G^k (Г)-структуры (см. G-структура).порядка k на М (первая основная теорема Картана). Классификация всех примитивных п. п. Ли бесконечного типа впервые была получена Э. Картаном [2]. Согласно его теореме всякая примитивная п. ц. Ли бесконечного типа, состоящая из голоморфных локальных преобразований, локально изоморфна одной из п. п. примеров 1)-6). Эта теорема неоднократно передоказывалась; ее современные доказательства получаются чисто алгебраич. средствами. При этом локальное изучение транзитивной п. п. Ли Г сводится к изучению нек-рой фильтрованной алгебры Ли (см. [9]). Классификация таких фильтрованных алгебр Ли может быть проведена на основе классификации простых градуированных алгебр Ли (см. [3]). Классификация примитивных п. п. Ли получена также и в вещественном случае, причем условие аналитичности действия п. п. заменено более слабым условием бесконечной дифференцируемости (см. [8], [9]).

Построены нек-рые абстрактные модели транзитивных п. п. Ли, к-рые призваны играть в теории п. п. бесконечного типа такую же роль, какую в конечномерном случае играют абстрактные группы Ли (см. [6], [9]).

Лит.:[1] Стернбер. <г С., Лекции по дифференциальной геометрии, пер. с англ., М., 1970; [2] Cartan Ё., Oeuvres completes, v. 2, P., 1953, p. 571 - 714 857-925; 1335-84; [3] Guillemin V., "J. Diff. Geom.", 1970, v. 4, № 3, p. 257-82; [4] Коbауashi S., Transformation groups in differential geometry. В.- [u. a.]. 1972; [5] Kobayashi S., Naganо Т., "J. Math, and Mech.">, 1964, v. 13, № 5, p. 875-907; 1965, v. 14, p. 679-706; [6] Кuranishi M., "Nagoya Math. J.", 1959, v. 15, p. 225-60; 1961, v. 19, p. 55 - 91; [7) Libermann P., "Bull. Soc. math. France", 1959, t. 87, № 4, p. 409-25; [8] Shnider S., "J. Diff. Geom.", 1970, v. 4, № 1, p. 81-89; [9] Singer I. M., Sternberg S., "J. d'Analyse math.", 1965, t. 15, p. 1 - 114; [10] Wi Iso n R. L., "Prop.. Amer. Math. Soc.", 1971, v. 29, № 2, p. 243 - 49. Э. В. Винберг.