ПРЕДСТАВЛЕНИЕ АЛГЕБРЫ ЛИ

в векторном пространстве V - гомоморфизм r алгебры Ли Lнад полем kв алгебру Ли 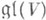всех линейных преобразований пространства Vнад k. Два представления и наз. эквивалентными (или изоморфными), если существует изоморфизм 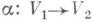, для к-рого

a(r₁ (l) v₁).r₂(l)a (v₁)

при любых . Представление r в Vназ. <конечномерным, если 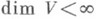, и неприводимым, если в Vне существует отличных от нуля и всего пространства подпространств, инвариантных относительно всех операторов .

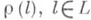При заданных представлениях и можно построить представления (прямая сумма) и (тензорное произведение) алгебры Lв пространствах и , полагая

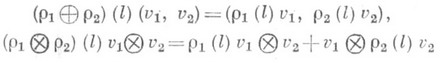
для . Если r - представление алгебры Ли Lв пространстве V, то формула

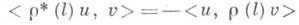
определяет представление r* алгебры Lна сопряженном к Vпространстве, наз. контраградиентным по отношению к r.

Каждое П. а. Ли Lоднозначно продолжается до представления универсальной обертывающей алгебры U(L);тем самым устанавливается изоморфизм категории П. а. Ли Lи категории модулей над U(L). В частности, представлению r алгебры Lсоответствует идеал в U(L) - ядро его продолжения 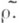Если представление р неприводимо, то идеал 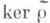примитивен. Обратно, всякий примитивный идеал в U(L).строится таким способом по нек-рому (вообще говоря, не единственному) неприводимому представлению r алгебры L. Изучение пространства примитивных идеалов PrimU(L), снабженного топологией Джекобсона, является существенной частью теории П. а. Ли. Оно проведено полностью в случае, когда L - конечномерная разрешимая алгебра Ли, а k-алгебраически замкнутое поле характеристики нуль (см. [2]).

Наиболее полно изучены конечномерные представления конечномерных алгебр Ли над алгебраически замкнутым полем характеристики нуль. В случае полей и 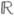эти представления находятся во взаимно однозначном соответствии с аналитическими конечномерными представлениями соответствующих односвязных (комплексных или вещественных) групп Ли. В этой ситуации любое представление разрешимой алгебры Ли содержит одномерное инвариантное подпространство (см. Ли теорема). Любое представление полупростой алгебры Ли вполне приводимо, т. е. изоморфно прямой сумме неприводимых представлений. Неприводимые представления полупростой алгебры Ли Lполностью классифицированы: классы изоморфных представлений взаимно однозначно соответствуют доминантным весам, т. е. весам с неотрицательными числовыми отметками, из сопряженного пространства Н* к подалгебре Картана Н алгебры L(см. Картана теорема о старшем векторе). Об описании строения неприводимого представления по соответствующему ему доминантному весу (его старшему весу) см. в статьях Кратность веса, Характеров формула.

Произвольный (не являющийся, вообще говоря, доминантным весом) элемент также определяет нек-рое неприводимое линейное представление полу простой алгебры Ли Lсо старшим весом l, являющееся, однако, бесконечномерным (см. Представление со старшим сектором). Соответствующие U(L)-модули наз. модулями Верма (см. [2]). Полной классификации неприводимых бесконечномерных представлений полупростых алгебр Ли пока (1983) не получено.

Если k - алгебраически замкнутое поле характеристики р>0, то неприводимые представления конечномерной алгебры Ли Lвсегда конечномерны и их размерность ограничена константой, зависящей от n=dim L. Если алгебра Lимеет р-структуру, то эта константа есть р ^{( п-r)/2}, где r - минимальная возможная размерность аннулятора линейной формы на Lв неприсоединением представлении [4]. Для описания множества неприводимых представлений в этом случае применяется следующая конструкция. Пусть Z(L) - центр алгебры U(L).и M_L- аффинное алгебраич. многообразие (размерность dim M_L=n), алгебра регулярных функций на к-ром совпадает с Z(L).(многообразие Цассенхауза). Отображение 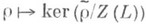позволяет сопоставить каждому неприводимому представлению точку многообразия Цассенхауза. Получаемое отображение сюръективно, прообраз любой точки из M_L конечен, а для точек открытого всюду плотного подмножества этот прообраз состоит из одного элемента [7]. Полное описание всех неприводимых представлений имеется для нильпотентных алгебр Ли (см. [8]) и нек-рых отдельных примеров [см. [9], [10]). Получены также разнообразные результаты относительно специальных типов представлений. Лит.:[1] Бурбаки Н., Группы и алгебры Ли, пер. с франц., М., 1976-78; [2] Диксмье Ж., Универсальные обертывающие алгебры, пер. с франц., М., 1978; [3] Джекобсон Н., Алгебры Ли, пер. с англ., М., 1964; [4] Мильнер А. А., "Функциональный анализ и его приложения", 1980, т. 14, № 2, с. 67-68; [5] Серр Ж. - П., Алгебры Ли и группы Ли, пер. с англ, и франц., М., 1969; [6] Теория алгебр Ли. Топология групп Ли, пер. с франц., М., 1962; [7] Zаssеnhаus H., "Proc. Glasgow Math. Assoc.", 1954, v. 2, p. 1-36; [8] Вейсфейлер Б. Ю., Кац В. Г., "Функциональный анализ и его приложения", 1971, т. 5, .№ 2, с. 28-36; [9] Jantzеn J. С., "Math. Z.", 1974, Bd 140, H. 1, S. 127-49; [10] Рудаков A. H., "Изв. АН СССР. Сер. матем.", 1970, т. 34, № 4, с. 735 - 43. А. Н. Рудаков.