- АФФИННАЯ СВЯЗНОСТЬ
дифференциально-геометрическая структура на гладком многообразии М, специальный вид связности на многообразии, когда приклеенное к Мгладкое расслоенное пространство
 имеет типовым слоем аффинное пространство
имеет типовым слоем аффинное пространство  размерности
размерности  . Структурой такого Ек каждой точке
. Структурой такого Ек каждой точке  присоединяется экземпляр аффинного пространства
присоединяется экземпляр аффинного пространства  , к-рый отождествляется с касательным центроаффинным пространством
, к-рый отождествляется с касательным центроаффинным пространством  . А. с. предусматривает такое сопоставление каждой гладкой кривой
. А. с. предусматривает такое сопоставление каждой гладкой кривой  с началом
с началом  и каждой ее точке
и каждой ее точке  аффинного отображения
аффинного отображения  , что удовлетворяется ниже сформулированное условие. Пусть Мпокрыто координатными областями, в каждой из к-рых фиксировано гладкое поле аффинного репера в
, что удовлетворяется ниже сформулированное условие. Пусть Мпокрыто координатными областями, в каждой из к-рых фиксировано гладкое поле аффинного репера в  , у к-рого начало совпадает с
, у к-рого начало совпадает с  (т. е. фиксированы пгладких векторных полей, линейно независимых в каждой точке
(т. е. фиксированы пгладких векторных полей, линейно независимых в каждой точке  области). Требуется, чтобы при
области). Требуется, чтобы при  , когда
, когда  перемещается по
перемещается по  до
до  , отображение
, отображение 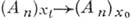 стремилось к тождественному отображению, причем главная часть его отклонения от последнего определялось относительно некоторого из реперов системой линейных дифференциальных форм
стремилось к тождественному отображению, причем главная часть его отклонения от последнего определялось относительно некоторого из реперов системой линейных дифференциальных форм

Итак, образом при
 репера в точке
репера в точке  является система из точки в
является система из точки в  с радиус-вектором
с радиус-вектором
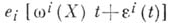 и пвекторов
и пвекторов  где X - касательный вектор к Lв точке х 0 , причем
где X - касательный вектор к Lв точке х 0 , причем 
Многообразие Мс заданной на ней А. с. наз. пространством аффинной связности. При преобразовании репера поля в произвольной точке
 согласно формулам
согласно формулам  т. е. при переходе к произвольному элементу главного расслоенного пространства Рреперов в касательных пространствах
т. е. при переходе к произвольному элементу главного расслоенного пространства Рреперов в касательных пространствах  с началами в точке
с началами в точке  , формы (1) заменяются следующими 1-формами на Р:
, формы (1) заменяются следующими 1-формами на Р:

а 2-формы

преобразуются так:

где
 и
и  составлены согласно (3) из форм (2). Уравнения (3) называются структурными уравнениями А. с. на М, где левые части - так наз.
составлены согласно (3) из форм (2). Уравнения (3) называются структурными уравнениями А. с. на М, где левые части - так наз.
кручения формы
 и кривизны формы
и кривизны формы - полубазовы, т. е. являются линейными комбинациями
- полубазовы, т. е. являются линейными комбинациями 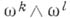 :
:

Любые 1-формы
 заданные на Ри удовлетворяющие уравнениям (3) с левыми частями вида (4), определяют нек-рую А. с. на М. Отображение
заданные на Ри удовлетворяющие уравнениям (3) с левыми частями вида (4), определяют нек-рую А. с. на М. Отображение  для кривой
для кривой  получается следующим ооразом: нужно выбрать нек-рое гладкое поле репера в координатной окрестности начала
получается следующим ооразом: нужно выбрать нек-рое гладкое поле репера в координатной окрестности начала 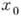 кривой L, п образ репера в точке
кривой L, п образ репера в точке  определить как решение
определить как решение  системы
системы

при начальных условиях

 - уравнения кривой L. Кривая, описываемая в
- уравнения кривой L. Кривая, описываемая в  точкой с радиус-вектором
точкой с радиус-вектором  относительно
относительно  , наз. разверткой кривой L. Поле репера в координатной окрестности можно выбрать так, чтобы
, наз. разверткой кривой L. Поле репера в координатной окрестности можно выбрать так, чтобы  тогда
тогда  На пересечении координатных окрестностей
На пересечении координатных окрестностей
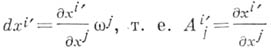
и

Здесь
 и
и  составляют, соответственно, кручения тензор и кривизны тензор А. с. на М. А. с. на Мможет быть задана системой функций
составляют, соответственно, кручения тензор и кривизны тензор А. с. на М. А. с. на Мможет быть задана системой функций  на каждой координатной окрестности, преобразующейся на пересечении окрестностей по формуле (5) - так наз. объектом А. с. Отображение
на каждой координатной окрестности, преобразующейся на пересечении окрестностей по формуле (5) - так наз. объектом А. с. Отображение  получается с помощью системы (5), в к-рую следует подставить
получается с помощью системы (5), в к-рую следует подставить

Если в нек-рой окрестности точки
 дано векторное поле
дано векторное поле  , то при
, то при  вектор
вектор  отображается в вектор
отображается в вектор  (где
(где 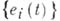 - решение системы (5)), дифференциал к-рого в
- решение системы (5)), дифференциал к-рого в 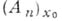 при
при  :
:
наз. ковариантным дифференциалом поля Xотносительно данной А. с. Здесь

образуют тензорное поле, наз. ковариантной производной поля
 Если дано второе векторное поле
Если дано второе векторное поле  то определяется ковариантная производная поля X в направлении Y:
то определяется ковариантная производная поля X в направлении Y:

к-рая относительно произвольного поля репера может быть определена также формулой

А. с. на Мможет быть задана и как билинейный оператор
 , к-рый двум векторным полям
, к-рый двум векторным полям  ставит в соответствие третье
ставит в соответствие третье  и обладает свойствами:
и обладает свойствами:

где f - гладкая функция на М. Связь с вышеуказанными способами задания устанавливается формулой:
 где
где  - поле репера; поля тензоров кручения и кривизны
- поле репера; поля тензоров кручения и кривизны

определяются формулами

Векторное поле
 наз. параллельным вдоль кривой
наз. параллельным вдоль кривой  , если
, если  тождественно относительно
тождественно относительно  , т. е. если вдоль
, т. е. если вдоль 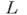

Параллельными векторными полями осуществляется параллельное перенесение векторов (и вообще тензоров) в А. с., представляющее собой линейное отображение касательных векторных пространств
 , определяемые отображением
, определяемые отображением  В этом смысле каждая А. с. порождает нек-рую линейную связность на М.
В этом смысле каждая А. с. порождает нек-рую линейную связность на М.
Кривая Lназ. геодезической линией в данной А. с., если ее развертка является прямой линией; другими словами, если в подходящей параметризации ее касательное векторное поле
 параллельно вдоль ее. Относительно локальной координатной системы геодезич. линии определяются системой
параллельно вдоль ее. Относительно локальной координатной системы геодезич. линии определяются системой

Через каждую точку в каждом направлении проходит одна геодезическая.
Существует взаимно однозначное соответствие между А. с. на Ми связностями в главных расслоенных пространствах свободных аффинных реперов в
 ими порождаемыми. Замкнутым кривым с началом и концом в хсоответствуют аффинные преобразования
ими порождаемыми. Замкнутым кривым с началом и концом в хсоответствуют аффинные преобразования  к-рые образуют неоднородную голономии группу данной А. с. Соответствующие линейные автоморфизмы
к-рые образуют неоднородную голономии группу данной А. с. Соответствующие линейные автоморфизмы  образуют однородную группу голономии. Согласно теореме о голономии алгебры Ли этих групп определяются 2-формами кручения
образуют однородную группу голономии. Согласно теореме о голономии алгебры Ли этих групп определяются 2-формами кручения 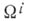 и кривизны
и кривизны  Для последних имеют место тождества Бианки:
Для последних имеют место тождества Бианки:
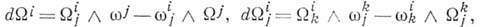
к-рые, в частности, для А. с. без кручения, когда
 сводятся к следующим:
сводятся к следующим:

Понятие А. с. возникло в 1917 в римановоп геометрии ( в виде Леви-Чивита связности);самостоятельный смысл оно обрело в 1918-24 в работах Г. Вейля [1] и Э. Картана [2].
Лит.:[1] Weyl H., Raum, Zeit, Materie, 5 Aufl.. В., 1923; [2] Сartan E., "Ann. sclent. Eсо1е norm, super.", 1923, т. 40, p. 325-412; 1924, t. 41, p. 1-25; 1925, t. 42, p. 17-88; [3] Кapтан Э., Пространства аффинной, проективной и конформной связности, пер. с франц., Казань, 1962; [4] Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967; [5] Постников М. М., Вариационная теория геодези-чееких, М., 1965. Ю. Г. Лумисте.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
