- ГОМОТОПИЧЕСКАЯ ГРУППА
обобщение фундаментальной группы, предложенное В. Гуревичем [1] в связи с задачей о классификации непрерывных отображений. Г. г. определены для любого
 . При
. При  Г. г. совпадает с фундаментальной группой. Определение Г. г. не конструктивно, и поэтому их вычисление является трудной задачей, общие методы решения к-рой были выработаны только в 50-х гг. 20 в. Значение Г. г. определяется тем, что все задачи теории гомотопий более или менее сводятся (см. Гомотопический тип).к задаче вычисления тех или иных Г. г.
Г. г. совпадает с фундаментальной группой. Определение Г. г. не конструктивно, и поэтому их вычисление является трудной задачей, общие методы решения к-рой были выработаны только в 50-х гг. 20 в. Значение Г. г. определяется тем, что все задачи теории гомотопий более или менее сводятся (см. Гомотопический тип).к задаче вычисления тех или иных Г. г.
Пусть

- единичный re-мерный куб,
 - его грань
- его грань  и
и  - объединение всех остальных его граней. Для любой пунктированной пары
- объединение всех остальных его граней. Для любой пунктированной пары  (см. Пунктированный объект).символом
(см. Пунктированный объект).символом  (или просто
(или просто  ) обозначается пунктированное множество всех гомотопич. классов [u] (см. Гомотопия).отображений
) обозначается пунктированное множество всех гомотопич. классов [u] (см. Гомотопия).отображений

отмеченным элементом (нулем) этого множества служит класс постоянного отображения, переводящего весь куб
 в точку
в точку  . Каждое непрерывное отображение
. Каждое непрерывное отображение

индуцирует нек-рый морфизм

пунктированных множеств. Для любого
 множества
множества  и морфизмы
и морфизмы  составляют нек-рый функторpn из категории пунктированных пар в категорию пунктированных множеств. Этот функтор гомотопически инвариантен, то есть
составляют нек-рый функторpn из категории пунктированных пар в категорию пунктированных множеств. Этот функтор гомотопически инвариантен, то есть  когда fи g гомотопны (как отображения пунктированных пар). Кроме того, он нормирован, в том смысле, что если
когда fи g гомотопны (как отображения пунктированных пар). Кроме того, он нормирован, в том смысле, что если 
При
 в множество
в множество  можно ввести операцию сложения, относительно к-рой оно будет группой (при n>2 даже абелевой): по определению, если
можно ввести операцию сложения, относительно к-рой оно будет группой (при n>2 даже абелевой): по определению, если  и
и  , то
, то  , где
, где  - отображение
- отображение

определенное формулой

Получающаяся группа
 наз. n-й гомотопической группой (или n-мерной Г. г.) пунктированной пары
наз. n-й гомотопической группой (или n-мерной Г. г.) пунктированной пары  ; говорят также о Г. г. пары (X, .А) в точке х 0 или о Г. г. пространства Xотносительно подпространства А в точке х 0. Отображения
; говорят также о Г. г. пары (X, .А) в точке х 0 или о Г. г. пространства Xотносительно подпространства А в точке х 0. Отображения  являются гомоморфизмами этих групп. Таким образом, при
являются гомоморфизмами этих групп. Таким образом, при  можно считать, что функтор
можно считать, что функтор  принимает значения в категории групп (при
принимает значения в категории групп (при  даже абелевых). При
даже абелевых). При  группа
группа  обозначается
обозначается  , или просто
, или просто  , и наз. абсолютной гомотопической группой пунктированного пространства
, и наз. абсолютной гомотопической группой пунктированного пространства  (или пространства Xв точке х 0 ). Ее элементами являются гомотопич. классы отображений
(или пространства Xв точке х 0 ). Ее элементами являются гомотопич. классы отображений  где
где 
 - граница куба
- граница куба  . Для таких отображений формула (1) имеет смысл и при и=1, так что множество
. Для таких отображений формула (1) имеет смысл и при и=1, так что множество  оказывается группой. Эта группа совпадает с классической фундаментальной группой. Обычно групповая операция в
оказывается группой. Эта группа совпадает с классической фундаментальной группой. Обычно групповая операция в  наз. умножением. Эта группа, вообще говоря, неабелева, тогда как группа
наз. умножением. Эта группа, вообще говоря, неабелева, тогда как группа  - абелева. Для любого
- абелева. Для любого  группы
группы  и соответствующие гомоморфизмы составляют нек-рый функтор из категории пунктированных пространств в категорию групп (при
и соответствующие гомоморфизмы составляют нек-рый функтор из категории пунктированных пространств в категорию групп (при  - в категорию абелевых групп). Этот функтор является композицией
- в категорию абелевых групп). Этот функтор является композицией  функтора вложения
функтора вложения  и построенного выше функтора
и построенного выше функтора  .
.
Функтор
 распространяется и на случай
распространяется и на случай  , если понимать под
, если понимать под  пунктированное множество компонент линейной связности пространства X;нулем этого множества является компонента, содержащая точку
пунктированное множество компонент линейной связности пространства X;нулем этого множества является компонента, содержащая точку  . Множество
. Множество  при
при  не определяется. Для упрощения формулировок множества
не определяется. Для упрощения формулировок множества  и
и  обычно также наз. Г. г., хотя они, вообще говоря, являются лишь пунктированными множествами.
обычно также наз. Г. г., хотя они, вообще говоря, являются лишь пунктированными множествами.
Для любого элемента
 отображение
отображение  представляет собой отображение
представляет собой отображение 
 и потому определяет нек-рый элемент Г. г.
и потому определяет нек-рый элемент Г. г.  Этот элемент зависит только от хи обозначается символом
Этот элемент зависит только от хи обозначается символом  . Получающееся отображение
. Получающееся отображение  является морфизыом пунктированных множеств (при
является морфизыом пунктированных множеств (при  - гомоморфизмом групп) и наз. граничным гомоморфизмом, или граничным оператором. Граничный гомоморфизм вместе с гомоморфизмами
- гомоморфизмом групп) и наз. граничным гомоморфизмом, или граничным оператором. Граничный гомоморфизм вместе с гомоморфизмами  и
и  , индуцированными вложениями
, индуцированными вложениями  и
и 
 позволяет написать бесконечную слева последовательность групп и гомоморфизмов:
позволяет написать бесконечную слева последовательность групп и гомоморфизмов:

Это - точная последовательность;она наз. точной гомотопической последовательностью пары
 и обозначается обычно
и обозначается обычно  . Если
. Если  для всех
для всех  , то гомоморфизм
, то гомоморфизм  является изоморфизмом (также для всех п).
является изоморфизмом (также для всех п).
Граничный гомоморфизм
 обладает свойством естественности, т. е. является морфизмом функтора
обладает свойством естественности, т. е. является морфизмом функтора  в функтор
в функтор  [точнее, в функтор
[точнее, в функтор  , где
, где 
 . Это позволяет определить
. Это позволяет определить  как функтор, принимающий значения в категории точных последовательностей пунктированных множеств, являющихся, за исключением последних шести множеств, абелевыми группами, а за исключением последних трех множеств,- группами.
как функтор, принимающий значения в категории точных последовательностей пунктированных множеств, являющихся, за исключением последних шести множеств, абелевыми группами, а за исключением последних трех множеств,- группами.
Пусть
 - произвольное расслоение в смысле Серра и пусть
- произвольное расслоение в смысле Серра и пусть  и
и  Отображение ропределяет нек-рое отображение
Отображение ропределяет нек-рое отображение 
 пунктированных пар. Для любого
пунктированных пар. Для любого  индуцированный этим отображением гомоморфизм
индуцированный этим отображением гомоморфизм  является изоморфизмом.
является изоморфизмом.
В частности, это верно при
 . В этом случае формула
. В этом случае формула  однозначно определяет нек-рый гомоморфизм
однозначно определяет нек-рый гомоморфизм  где
где  - слой расслоения рнад точкой
- слой расслоения рнад точкой  . Этот гомоморфизм наз. гомотопической трансгрессией. Он входит в точную последовательность
. Этот гомоморфизм наз. гомотопической трансгрессией. Он входит в точную последовательность

Эта последовательность наз. гомотопической последовательностью расслоения
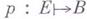 . Сопоставление расслоению его гомотопич. последовательности приводит к нек-рому функтору на категории всех (пунктированных) расслоений.
. Сопоставление расслоению его гомотопич. последовательности приводит к нек-рому функтору на категории всех (пунктированных) расслоений.
В частном случае, когда ресть стандартнее Серра расслоение путей над пространством X, для любого
 имеет место изоморфизм
имеет место изоморфизм  . где
. где  - петель пространство пространства X. Этот изоморфизм наз. изоморфизмом Гуревича.
- петель пространство пространства X. Этот изоморфизм наз. изоморфизмом Гуревича.
Перечисленные свойства по существу однозначно определяют Г. г.
 т. е. могут быть приняты за аксиомы, описывающие эти Г. г. Именно, пусть
т. е. могут быть приняты за аксиомы, описывающие эти Г. г. Именно, пусть  - произвольная последовательность гомотопически инвариантных нормированных функторов, заданных на категории пунктированных пространств, принимающих значения в категории пунктированных множеств и обладающих тем свойством, что для любого расслоения в смысле Серра
- произвольная последовательность гомотопически инвариантных нормированных функторов, заданных на категории пунктированных пространств, принимающих значения в категории пунктированных множеств и обладающих тем свойством, что для любого расслоения в смысле Серра  любого подмножества
любого подмножества  и любой точки
и любой точки  индуцированный гомоморфизм
индуцированный гомоморфизм  является изоморфизмом. Такая последовательность наз. гомотопической системой, если для любого
является изоморфизмом. Такая последовательность наз. гомотопической системой, если для любого  задан морфизм
задан морфизм  функтора
функтора  в функтор
в функтор  (при
(при  - в
- в  ), являющийся изоморфизмом для любой пунктированной пары
), являющийся изоморфизмом для любой пунктированной пары  , для которой
, для которой  при всех
при всех  . Любая гомотопич. система изоморфна построенной выше гомотопич. системе, состоящей из Г. г. Более того, при
. Любая гомотопич. система изоморфна построенной выше гомотопич. системе, состоящей из Г. г. Более того, при  в пунктированные множества
в пунктированные множества  (а также в множества
(а также в множества  ) можно единственным образом ввести групповое строение (структуру группы) так, чтобы все мор-физмы
) можно единственным образом ввести групповое строение (структуру группы) так, чтобы все мор-физмы  были гомоморфизмами [это строение совпадает, стало быть, с тем, к-рое определяется формулой (1)]. В группах же
были гомоморфизмами [это строение совпадает, стало быть, с тем, к-рое определяется формулой (1)]. В группах же  при
при  и
и  можно только ввести еще инверсную групповую операцию. Все это и означает, что перечисленные выше свойства однозначно определяют Г. г. (с точностью до порядка сомножителей в некоммутативных группах).
можно только ввести еще инверсную групповую операцию. Все это и означает, что перечисленные выше свойства однозначно определяют Г. г. (с точностью до порядка сомножителей в некоммутативных группах).
Для любого отображения
 и любого пути
и любого пути  , соединяющего точку
, соединяющего точку  с точкой
с точкой  , формула
, формула  определяет нек-рую гомо-топию отображения
определяет нек-рую гомо-топию отображения  . По аксиоме о распространении гомотопии (см. Корасслоение).эта гомотопия может быть распространена до нек-рой гомотопии
. По аксиоме о распространении гомотопии (см. Корасслоение).эта гомотопия может быть распространена до нек-рой гомотопии  обладающей тем свойством, что
обладающей тем свойством, что  . Конечное отображение u1 этой гомотопии переводит
. Конечное отображение u1 этой гомотопии переводит  в
в  , то есть представляет собой отображение
, то есть представляет собой отображение 
Соответствующий элемент Г. г.
 зависит только от класса
зависит только от класса  отображения ии гомотопич. класса
отображения ии гомотопич. класса  пути
пути  и обозначается символом
и обозначается символом  (при n=1 - символом
(при n=1 - символом  ). Семейство
). Семейство  определяется тем самым как локальное семейство на пространстве X, т. е. на фундаментальном группоиде этого пространства. В частности, для любой точки
определяется тем самым как локальное семейство на пространстве X, т. е. на фундаментальном группоиде этого пространства. В частности, для любой точки  группа
группа 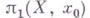 оказывается группой операторов группы
оказывается группой операторов группы  . При
. При  эти операторы действуют как внутренние автоморфизмы:
эти операторы действуют как внутренние автоморфизмы:  , а при
, а при  определяют группу
определяют группу  как
как  -модуль. Для любого непрерывного отображения
-модуль. Для любого непрерывного отображения  индуцированные гомоморфизмы
индуцированные гомоморфизмы  являются операторными гомоморфизмами (гомоморфизмами модулей):
являются операторными гомоморфизмами (гомоморфизмами модулей): .
.
Аналогичным образом группы
 составляют локальное семейство Г. г. на подпространстве А . В частности,
составляют локальное семейство Г. г. на подпространстве А . В частности,  является группой операторов Г. г.
является группой операторов Г. г.  , так что при
, так что при  группа
группа 
 будет
будет  - модулем. Группа
- модулем. Группа  является скрещенным
является скрещенным  - модулем (см. Скрещенные модули), где
- модулем (см. Скрещенные модули), где  - граничный гомоморфизм.
- граничный гомоморфизм.
Группа
 служит группой операторов не только групп
служит группой операторов не только групп  , но и групп
, но и групп  , а также, в силу естественного гомоморфизма
, а также, в силу естественного гомоморфизма 
 -группой операторов групп
-группой операторов групп  Относительно этого действия группы
Относительно этого действия группы  все гомоморфизмы точной последовательности
все гомоморфизмы точной последовательности  являются операторными гомоморфизмами, так что группа
являются операторными гомоморфизмами, так что группа  может рассматриваться как группа операторов последовательности
может рассматриваться как группа операторов последовательности  Это равносильно тому, что последовательности
Это равносильно тому, что последовательности  составляют локальное семейство точных последовательностей на подпространстве А.
составляют локальное семейство точных последовательностей на подпространстве А.
В случае, когда дополнение
 представляет собой объединение непересекающихся открытых n-мерных клеток,
представляет собой объединение непересекающихся открытых n-мерных клеток,  -модуль
-модуль  является свободным модулем (при
является свободным модулем (при  - свободным скрещенным модулем) и обладает системой свободных образующих - базисом, находящимся в биективном (не обязательно естественном) соответствии с клетками из
- свободным скрещенным модулем) и обладает системой свободных образующих - базисом, находящимся в биективном (не обязательно естественном) соответствии с клетками из  (теорема Уайтхеда).
(теорема Уайтхеда).
Отображения
 находятся в биективном соответствии с отображениями
находятся в биективном соответствии с отображениями  где
где  - произвольная n-мерная сфера, а
- произвольная n-мерная сфера, а  - нек-рая ее точка; поэтому элементы группы
- нек-рая ее точка; поэтому элементы группы  можно рассматривать как гомотопич. классы отображений
можно рассматривать как гомотопич. классы отображений  Это верно и при n=0. Указанное отождествление зависит от выбора нек-рого относительного гомеоморфизма
Это верно и при n=0. Указанное отождествление зависит от выбора нек-рого относительного гомеоморфизма  . Обычно сфера Sn и гомеоморфизм j предполагаются раз навсегда выбранными и фиксированными. В первоначальном, ставшем малоупотребительным определении Гуревича, сфера
. Обычно сфера Sn и гомеоморфизм j предполагаются раз навсегда выбранными и фиксированными. В первоначальном, ставшем малоупотребительным определении Гуревича, сфера  не фиксировалась, а гомеоморфизм
не фиксировалась, а гомеоморфизм  задавался с точностью до гомотопии. Такое задание гомеоморфизма
задавался с точностью до гомотопии. Такое задание гомеоморфизма  равносильно заданию нек-рой ориентации сферы
равносильно заданию нек-рой ориентации сферы  Таким образом, по Гуревичу, элементами группы
Таким образом, по Гуревичу, элементами группы  являются пунктированные гомотопич. классы отображений ориентированной re-мерной сферы в пространстве X. Множество
являются пунктированные гомотопич. классы отображений ориентированной re-мерной сферы в пространстве X. Множество  непунктированных гомотопич. классов отображений
непунктированных гомотопич. классов отображений  находится в биективном соответствии с орбитами, действия группы
находится в биективном соответствии с орбитами, действия группы  в группе
в группе  . Если
. Если  (или, более общим образом, если группа
(или, более общим образом, если группа  тривиально действует на группе
тривиально действует на группе  , - в этом случае пространство
, - в этом случае пространство  наз. гомотопически п- простым), то
наз. гомотопически п- простым), то  не зависит от точки
не зависит от точки  (так что в этом случае обозначение
(так что в этом случае обозначение  полностью оправдано). Эта группа естественным образом отождествляется с множеством
полностью оправдано). Эта группа естественным образом отождествляется с множеством  , к-рое является, стало быть, в этом случае группой. Пространство, гомотопическн n-простое для всех и, наз. абелевым.
, к-рое является, стало быть, в этом случае группой. Пространство, гомотопическн n-простое для всех и, наз. абелевым.
Пусть sn - ориентирующий класс гомологии сферы Sn и пусть
 . Тем самым определяется нек-рый гомоморфизм
. Тем самым определяется нек-рый гомоморфизм 
 , наз. гомоморфизмом Гуревича. Его ядро содержит все элементы вида
, наз. гомоморфизмом Гуревича. Его ядро содержит все элементы вида 
 (при
(при  - все элементы вида
- все элементы вида 
 т. е. содержит коммутант
т. е. содержит коммутант  группы
группы  ). Классич. теорема Пуанкаре утверждает, что при n=1 ядро гомоморфизма hсовпадает с коммутантом
). Классич. теорема Пуанкаре утверждает, что при n=1 ядро гомоморфизма hсовпадает с коммутантом  , так что группа
, так что группа  изоморфна про-коммутированной фундаментальной группе
изоморфна про-коммутированной фундаментальной группе  Обобщением теоремы Пуанкаре на случай n>1 является теорема Гуревича, утверждающая, что если
Обобщением теоремы Пуанкаре на случай n>1 является теорема Гуревича, утверждающая, что если  при
при  , то гомоморфизм h:
, то гомоморфизм h: является изоморфизмом (а гомоморфизм
является изоморфизмом (а гомоморфизм 
 - эпиморфизмом).
- эпиморфизмом).
Аналогичным образом элементы группы
 можно рассматривать как (пунктированные) гомотопич. классы отображений
можно рассматривать как (пунктированные) гомотопич. классы отображений  где
где  - (ориентированный) n-мерный шар, a S - его граница. Если пара
- (ориентированный) n-мерный шар, a S - его граница. Если пара  гомотопически n-проста [т. е. группа
гомотопически n-проста [т. е. группа  тривиально действует на группе
тривиально действует на группе 
 то в этом определении пунктированность можно игнорировать. Формула
то в этом определении пунктированность можно игнорировать. Формула

где
 - ориентирующий класс гомологии пары
- ориентирующий класс гомологии пары 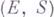 , а
, а  определяет гомоморфизм Гуревича
определяет гомоморфизм Гуревича

Если
 при
при  то этот гомоморфизм является изоморфизмом (теорема Гуревича для относительных групп).
то этот гомоморфизм является изоморфизмом (теорема Гуревича для относительных групп).
Для вычисления Г. г. конкретных пространств известны два основных метода: метод убивающих пространств и метод гомотопич. резольвент (см. Гомотопический тип, Постникова системы). Первый метод основывается на изоморфизме
 вытекающем из теоремы Гуревича, и определении убивающего пространства
вытекающем из теоремы Гуревича, и определении убивающего пространства  Этот изоморфизм сводит задачу вычисления группы
Этот изоморфизм сводит задачу вычисления группы  к задаче вычисления групп гомологии
к задаче вычисления групп гомологии  Пространство
Пространство  расслаивается над пространством
расслаивается над пространством  со слоем
со слоем  а группы гомологии пространств
а группы гомологии пространств  известны. Поэтому индукцией можно пытаться найти нужные группы гомологии убивающих пространств. Задача вычисления группы гомологии расслоенного пространства по группам гомологии его базы и слоя в общем виде полностью не решена (и, по-видимому, общего удовлетворительного решения не имеет), однако обширную информацию о группах гомологии пространств
известны. Поэтому индукцией можно пытаться найти нужные группы гомологии убивающих пространств. Задача вычисления группы гомологии расслоенного пространства по группам гомологии его базы и слоя в общем виде полностью не решена (и, по-видимому, общего удовлетворительного решения не имеет), однако обширную информацию о группах гомологии пространств 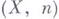 можно извлечь из соответствующих спектральных последовательностей Серра. Во многих случаях этой информации достаточно для вычисления групп
можно извлечь из соответствующих спектральных последовательностей Серра. Во многих случаях этой информации достаточно для вычисления групп  , по крайней мере для нек-рых n. Существенное технич. упрощение задачи достигается на основе серровской теории классов абелевых групп и вытекающей из этой теории теоремы
, по крайней мере для нек-рых n. Существенное технич. упрощение задачи достигается на основе серровской теории классов абелевых групп и вытекающей из этой теории теоремы  -аппроксимации, позволяющей проводить все вычисления во-первых для когомологий, а во-вторых лишь для групп коэффициентов
-аппроксимации, позволяющей проводить все вычисления во-первых для когомологий, а во-вторых лишь для групп коэффициентов  . Геометрич. принципы, лежащие в основе этой техники, были недавно вскрыты Дж. Адамсом (J. Adams) и Д. Саллнваном (D. Sullivan) [8] на основе понятия локализации топологич. пространств по данному простому р.
. Геометрич. принципы, лежащие в основе этой техники, были недавно вскрыты Дж. Адамсом (J. Adams) и Д. Саллнваном (D. Sullivan) [8] на основе понятия локализации топологич. пространств по данному простому р.
Второй (также индуктивный) метод вычисления Г. г. состоит в постепенном построении гомотопич. резольвенты пространства X. Пусть уже известен n-й член этой резольвенты [напр., если
 , то
, то  ].
].
Следующий член
 должен быть расслоенным пространством над Х п со слоем
должен быть расслоенным пространством над Х п со слоем  , причем группа
, причем группа  должна быть изоморфна известной группе
должна быть изоморфна известной группе  . Это дает (на основе соответствующей спектральной последовательности) определенную информацию о группе
. Это дает (на основе соответствующей спектральной последовательности) определенную информацию о группе  , позволяющую во многих случаях полностью ее вычислить. Напр., при
, позволяющую во многих случаях полностью ее вычислить. Напр., при  этим методом можно найти группы
этим методом можно найти группы  для всех
для всех  . В современной своей форме эти вычисления также основываются на понятии локализации.
. В современной своей форме эти вычисления также основываются на понятии локализации.
Метод гомотопич. резольвент был доведен (см. [5]) до алгоритма, применимого к любому односвязному конечному клеточному разбиению и дающего все его Г. г. Однако этот алгоритм для практич. применения слишком сложен.
Поскольку гомотопич. теория пространств полностью эквивалентна гомотопич. теории симплициальных множеств, определение Г. г. может быть перенесено на любые (полные) симплпциальные множества. Получающееся "комбинаторное" определение Г. г. (принадлежащее Д. Кану) легко может быть доведено до алгоритма. Однако и этот алгоритм для практич. вычислений слишком сложен.
Любой из описанных методов без труда устанавливает, что Г. г. произвольного односвязного пространства, имеющего конечно порожденные группы гомологии, также конечно порождены. Аналогичное утверждение для неодносвязных пространств (Г. г. конечно порождены как
 -модули), вообще говоря, неверно.
-модули), вообще говоря, неверно.
Пусть S- функтор (приведенной) надстройки, а
 - функтор петель. Так как эти функторы сопряжены, то для любого
- функтор петель. Так как эти функторы сопряжены, то для любого  тождественное отображение
тождественное отображение  определяет нек-рое вложение
определяет нек-рое вложение  . Поскольку
. Поскольку  это вложение определяет нек-рый гомоморфизм известный как гомоморфизм
это вложение определяет нек-рый гомоморфизм известный как гомоморфизм  надстройки. Он совпадает с гомоморфизмом, получающимся при сопоставлении произвольному (пунктированному) отображению
надстройки. Он совпадает с гомоморфизмом, получающимся при сопоставлении произвольному (пунктированному) отображению 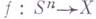 его надстройки
его надстройки 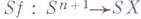 . Этот гомоморфизм входит в точную последовательность
. Этот гомоморфизм входит в точную последовательность

Эта последовательность наз. надстроечной последовательностью пространствa X. Фигурирующий в ней гомоморфизм Нявляется обобщением классического Хопфа инварианта.
В случае, когда X- счетное одновершинное клеточное разбиение, пространство
 может быть заменено (см. [7]) приведенной степенью
может быть заменено (см. [7]) приведенной степенью  разбиения X. Это показывает, что если
разбиения X. Это показывает, что если  при
при  , то гомоморфизм Еявляется изоморфизмом для всех
, то гомоморфизм Еявляется изоморфизмом для всех  и эпиморфизмом при
и эпиморфизмом при  . Эта теорема известна как теорема Фрейденталя о надстройке [Г. Фрейденталь (Н. Freudenthal) первым опубликовал доказательство для случая
. Эта теорема известна как теорема Фрейденталя о надстройке [Г. Фрейденталь (Н. Freudenthal) первым опубликовал доказательство для случая  , хотя теорема была известна и ранее].
, хотя теорема была известна и ранее].
Теорема Фрейденталя показывает, что при
 группа
группа  не зависит от п. Она наз. k-й стационарной Г. г. (стабильной Г. г.) сфер. Аналогичное явление стабилизации наблюдается для Г. г. ортогональных групп, Г. г. Тома пространств MSO и во многих других случаях. Общее изучение этого явления наиболее удобно проводить в рамках так наз. теории спектров. В этой теории стационарные Г. г. появляются как Г. г. спектров. Эти группы устроены существенно проще Г. г. пространства и их изучение (и вычисление) оказывается значительно более легкой задачей. Напр., для вычисления этих групп имеется специальный аппарат: спектральная последовательность Адамса.
не зависит от п. Она наз. k-й стационарной Г. г. (стабильной Г. г.) сфер. Аналогичное явление стабилизации наблюдается для Г. г. ортогональных групп, Г. г. Тома пространств MSO и во многих других случаях. Общее изучение этого явления наиболее удобно проводить в рамках так наз. теории спектров. В этой теории стационарные Г. г. появляются как Г. г. спектров. Эти группы устроены существенно проще Г. г. пространства и их изучение (и вычисление) оказывается значительно более легкой задачей. Напр., для вычисления этих групп имеется специальный аппарат: спектральная последовательность Адамса.
Г. г. обобщались в самых различных направлениях. Напр., делались попытки заменить сферы другими пространствами. Здесь можно отметить торусные Г. г., позволившие проинтерпретировать Уайтхеда произведения как нек-рые коммутанты. Показано также, что в множество гомотопич. классов отображений
 тогда и только тогда можно ввести естественную по Yгрупповую операцию, когда Xявляется ко-Н-пространством. Были определены Г. г. с коэффициентами, получающиеся при замене сфер
тогда и только тогда можно ввести естественную по Yгрупповую операцию, когда Xявляется ко-Н-пространством. Были определены Г. г. с коэффициентами, получающиеся при замене сфер  Мура пространствами,
Мура пространствами,  Это определение Г. г. с коэффициентами оказалось не очень удачным. Более удовлетворительное определение (согласующееся с общим принципом двойственности Экмана - Хилтона) было получено при замене M-пространств Мура ко-M-пространствами. Однако эти Г. г. определены не для всех G (напр., при G, являющейся аддитивной группой действительных чисел, эти группы не определены).
Это определение Г. г. с коэффициентами оказалось не очень удачным. Более удовлетворительное определение (согласующееся с общим принципом двойственности Экмана - Хилтона) было получено при замене M-пространств Мура ко-M-пространствами. Однако эти Г. г. определены не для всех G (напр., при G, являющейся аддитивной группой действительных чисел, эти группы не определены).
Детально изучен также вопрос о построении Г. г. в категориях, отличных от категории пунктированных пар. Здесь в первую очередь следует отметить построение Г. г. триад (см., напр., [3]), оказавшихся очень полезными при изучении гомоморфизма Е. Весьма общие конструкции Г. г. были предложены в связи с исследованиями по двойственности. На основе понятия стандартной конструкции (см. [6]) построение Г. г. было перенесено на произвольные категории. Существенную роль в этом построении играют уже упоминавшиеся Г. г. симплициальных множеств.
Лит.:[1] Стинрод Н., Топология косых произведений, пер. с англ., М., 1953; [2] Болтянский В. Г., Гомотопическая теория непрерывных отображений и векторных полей, М., 1955; [3] Ху Сы - дзян, Теория гомотопий пер. с англ., М., 1964; [4] Браун Э. X., "Математика" 1958, т. 2: 2, с.3-24; [5] Кан Д., там же, 1962 т. 6, № 1, с. 3-32; [6] Столлингс Дж., там же 1964, 8:4, с. 155-57; [7] Экман Б., Xилтон П. там же, 1960, 4 : 3, с. 3-27; [8] Сулливан Д., Геометрическая топология, пер. с англ., М., 1975. М. М. Постников.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
