- АЛГЕБРА МЕР
- алгебра М(G).комплексных регулярных борелевских мер на локально компактной абелевой группе G, имеющих ограниченную вариацию, с обычными линейными операциями и сверткой в качестве умножения (см. Гармонический анализ абстрактный). Свертка
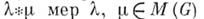полностью определяется из условия, что для любой непрерывной функции f на Gс компактным носителем
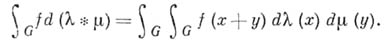
Если за норму в М(G).принять полную вариацию меры, то М(G).становится коммутативной банаховой алгеброй над полем комплексных чисел. А. м. М(G).обладает единицей, к-рой служит
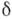-мера, сосредоточенная в нуле группы. Совокупность дискретных мер, содержащихся в M(G), образует замкнутую подалгебру.
Каждой функции f, принадлежащей групповой алгебре
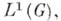может быть поставлена в соответствие мера 
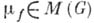по правилу
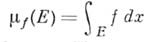
(интеграл по мере Хаара). При этом возникает изометрическое изоморфное вложение
Образ при этом вложении является замкнутым идеалом в M(G). Преобразованием Фурье - Стилтьеса меры 
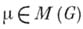наз. функция m на двойственной группе 
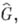определяемая формулой:
При этом
В частности, М(G).есть алгебра без радикала.
Если группа G не дискретна, то А. м. М(G).устроена весьма сложно: она не симметрична, и ее пространство максимальных идеалов обладает рядом патологич. свойств. Напр., это пространство содержит бесконечномерные аналитич. образования, а естественно вложенная в него группа
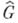не плотна даже в границе Шилова. Вместе с тем известны идемпотентные меры, т. е. такие, что 
Каждая идемпотентная мера есть конечная целочисленная комбинация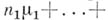 
причем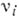 
-мера Хаара компактной подгруппы, а 
- характер. В случае 
это приводит к тому, что последовательность 
из 0 и 1 тогда и только тогда есть преобразование Фурье - Стилтьеса нек-рой меры на окружности, когда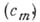 
не более чем в конечном числе членов отличается от периодич. последовательности.
В общем случае теорема об идемпотентных мерах допускает естественную интерпретацию в терминах нульмерных когомологий пространства максимальных идеалов. Удовлетворительное описание известно и для других групп когомологий пространства максимальных идеалов А. м., что, в частности, позволяет судить о возможности логарифмировать обратимую меру из М(G).(одномерные целочисленные когомологий).
Лит.:[1] Rudin W., Fourier analysis on groups, N.Y.- L., 1962; [2] Тау1оr J. L., "Acta math.", 1971, v. 126, № 3-4, p. 195-225. Е. А. Горин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
