- Голономные системы
-
механические системы, в которых все связи (см. Связи механические) являются геометрическими (голономными), то есть налагающими ограничения только на положения (или перемещения за время движения) точек и тел системы, но не на величины их скоростей. Например, двойной маятник (рис. а) является Г. с.; в нём связи (нити) налагают ограничения только на положения или перемещения грузов M1 и M2, но не на их скорости, которые при движении могут иметь любые значения. Связь, налагающая ограничения на скорости точек и тел системы, то есть устанавливающая между этими скоростями определённые соотношения, называется кинематической. Однако если эти соотношения можно свести к геометрическим, то есть к соотношениям между перемещениями (или координатами) точек и тел системы, то такая связь также является голономной. Например, при качении без скольжения колеса радиуса R по прямолинейному рельсу (рис. б) скорость υ центра колеса и угловая скорость ω колеса связаны соотношением υ=Rω, но его можно свести к геометрическому соотношению s = Rφ между перемещением s = AA1 центра и углом поворота φ колеса. Следовательно, это Г. с.Кинематические связи, не сводящиеся к геометрическим, называются неголономными, а механические системы с такими связями — неголономными системами (См. Неголономные системы). Разделение механических систем на голономные и неголономные очень существенно, так как ряд уравнений, позволяющих сравнительно просто решать задачи механики (например, Лагранжа уравнения механики), применим только к Г. С.С. М. Тарг.
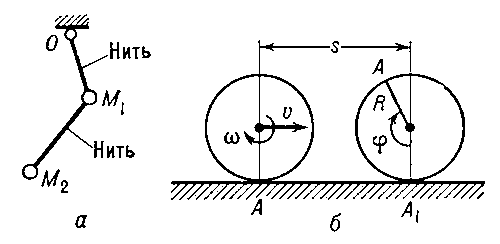 Рис. к ст. Голономные системы.
Рис. к ст. Голономные системы.
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
