Неявные функции

        функции, заданные соотношениями между независимыми переменными, не разрешенными относительно последних; эти соотношения являются одним из способов задания функции. Например, соотношение

         x² + y² - 1 = 0

        задаёт Н. ф.

         y = у (х),

        соотношения

         x = ρcosφsinϑ, y = ρsinφsinϑ, z = ρcosϑ

        задают Н. ф.:

         ρ = ρ(x, у, z), φ = φ(x, y, z), ϑ = ϑ(х, у, z).

        В простейших случаях соотношения, задающие Н. ф., могут быть разрешены в классе элементарных функций (См. Элементарные функции), т. е. удаётся найти элементарные функции, удовлетворяющие этим соотношениям. Так, в первом из приведённых выше примеров имеем:

        

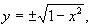        а во втором:

        

         Вообще же таких элементарных функций найти не удаётся. Н. ф. могут быть как однозначными, так и многозначными. Не всякое соотношение (или система соотношений) между переменными задаёт Н. ф. Так, если ограничиваться лишь действительными значениями переменных, то соотношение x² + y² + 1 = 0 не задаёт Н. ф., так как не удовлетворяется ни одной парой действительных значений х и у; соотношение же e^xy = 0 вообще не удовлетворяется ни одной парой действительных или комплексных значений х и у. Теорема существования Н. ф. в её простейшей формулировке утверждает, что если функция F (x, y) обращается в нуль при паре значений х = x₀, у = y₀ [F (x₀, y₀) ≠ 0] и дифференцируема в окрестности точки (x₀, y₀), причём F’_x (х, у) и F’_y (х, у) непрерывны в этой окрестности и F’_y (x₀, y₀) ≠ 0, то в достаточно малой окрестности точки x₀ существует одна и только одна однозначная непрерывная функция у = у (х), удовлетворяющая соотношению F (x, y) = 0 и обращающаяся в y₀ при x = x₀; при этом y'(x) = —F’_x (x, y)/F’_y (x, у).

         Для приближённого вычисления значений Н. ф. вблизи точки x₀, где её значение y₀ уже известно, широко применяются степенные ряды. Так, если F (x, у) — аналитическая функция [т. е. может быть разложена в окрестности точки (x₀, y₀) в сходящийся двойной степенной ряд] и F’_y (x₀, y₀) ≠ 0, то Н. ф., заданная соотношением F (x, y) = 0, может быть получена в виде степенного ряда

        

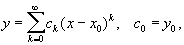        сходящегося в некоторой окрестности точки х = х₀. Коэффициенты c_k, k = 1, 2,..., могут быть найдены либо подстановкой этого ряда в соотношение F (x, у) = 0, либо последовательным дифференцированием этого соотношения по х. Например, если Н. ф. задана соотношением

         y⁵ + xy - 1 = 0, x₀ = 0, y₀ = 1,

        то

        

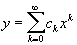        и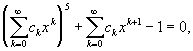

        

        откуда

         c₀ = 1, c₁ = —¹/₅c₀^-3, c₂ = —2c₁²c₀^-1 — ¹/₅c₁c₀^-4 = —¹/₂₅ и т.д.

         Если соотношение F (x, у) = 0 может быть представлено в виде у = а + хφ(у), где φ(y) — аналитическая функция, то Н. ф. у = у (х), заданная этим соотношением и принимающая значение а при х = 0, разлагается в ряд Лагранжа

        

        сходящийся в некоторой окрестности точки х = 0. Например, из соотношения у = а + xsiny (так называемое Кеплера уравнение) можно получить: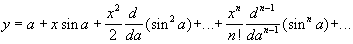

        

         Вычисление значений Н. ф. в общем случае может быть произведено по методу последовательных приближений.

         Лит.: Смирнов В. И., Курс высшей математики, т. 1, 22 изд., М., 1967; т. 3, ч. 2, 8 изд., М., 1969; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 1, М., 1969; Кудрявцев Л. Д., Математический анализ, т. 2, М., 1970.