Лорана ряд

Лорана ряд
        Ряд вида
        , (*)
        , (*)
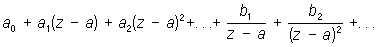        то есть ряд, расположенный как по положительным, так и по отрицательным степеням разности z — а (где z, а и коэффициенты ряда — комплексные числа). Совокупность членов с неотрицательными степенями представляет здесь обыкновенный Степенной ряд, сходящийся, вообще говоря, внутри круга с центром а и радиусом R (≤ ∞); остальные члены образуют ряд, сходящийся, вообще говоря, вне круга с тем же центром, но с радиусом r (r ≥ 0). Если r < R, то ряд (*) сходится в круговом кольце r < |z — а| < R; его сумма является в этом кольце аналитической функцией (См. Аналитические функции) комплексного переменного z.
         Несмотря на то, что ряды вида (*) встречаются уже у Л. Эйлера (1748), они получили своё название по имени П. Лорана, который в 1843 показал, что всякая функция комплексного переменного, однозначная и аналитическая в кольце r < |z — а| < R, может быть разложена в этом кольце в такой ряд (это так называемая теорема Лорана). Впрочем, ту же теорему получил несколько раньше К. Вейерштрасс, но его работа была опубликована лишь в 1894.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

Смотреть что такое "Лорана ряд" в других словарях:

  • ЛОРАНА РЯД — ряд, представляющий аналитическую функцию в окрестности её изолиров. особой точки. Получил своё назв. по имени П. Лорана (P. Laurent). Если z0 изолиров. особая точка аналитич. ф ции f(z), то в окрестности z0 ф ция f(z) представляется в виде суммы …   Физическая энциклопедия

  • Лорана ряд — Ряд Лорана  двусторонне бесконечный степенной ряд по целым степеням (z − a), то есть ряд вида Этот ряд понимается как сумма двух рядов:   правильная часть ряда Лорана и   главная часть ряда Лорана. При этом, ряд Лорана считается сходящимся тогда… …   Википедия

  • ЛОРАНА РЯД — обобщение степенного ряда по целым неотрицательным степеням разности z а или по целым неположительным степеням z а в виде Ряд (1) понимается как сумма двух рядов: правильная часть Л. р. и главная часть Л. р. Ряд (1) считается сходящимся тогда и… …   Математическая энциклопедия

  • ГАРТОГСА - ЛОРАНА РЯД — ряд где функции, голоморфные в нек рой не зависящей от kобласти Если для всех , то ряд (*) наз. рядом Гартогса. Всякая функция, голоморфная в Гартогса области D вида разлагается в абсолютно и равномерно сходящийся внутри DГ. Л. р. В полных… …   Математическая энциклопедия

  • Ряд Лорана — Ряд Лорана  двусторонне бесконечный степенной ряд по целым степеням , то есть ряд вида Этот ряд понимается как сумма двух рядов:   положительная часть ряда Лорана (иногда называется правильной) и   отрицательная часть ряда Лорана… …   Википедия

  • Ряд Тейлора — Ряд Тейлора  разложение функции в бесконечную сумму степенных функций. Ряд назван в честь английского математика Брука Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора  его использовали ещё в XVII веке Грегори, а… …   Википедия

  • Правильная часть ряда Лорана — Ряд Лорана  двусторонне бесконечный степенной ряд по целым степеням (z − a), то есть ряд вида Этот ряд понимается как сумма двух рядов:   правильная часть ряда Лорана и   главная часть ряда Лорана. При этом, ряд Лорана считается сходящимся тогда… …   Википедия

  • Многочлен Лорана — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… …   Википедия

  • ДИРИХЛЕ РЯД — для аналитической почти периодической функции ряд вида представляющий собой все ряды Фурье аналитической регулярной почти периодической в полосе (a, b), , функции f(s)=f(t+it) на конти . нуальной совокупности прямых R(s) = t (см. Почти… …   Математическая энциклопедия

  • ВЫЧЕТ — аналитической функции f(z) одного комплексного переменного в конечной изолированной особой точке аоднозначного характера коэффициент при в разложении Лорана функции f(z) (см. Лорана ряд).в окрестности точки а, или равный ему интеграл где… …   Математическая энциклопедия

Книги



Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»