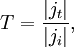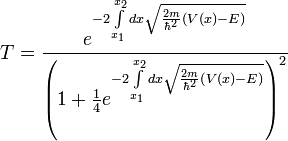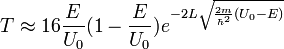- Коэффициент отражения
-
В нерелятивистской квантовой механике коэффициент прохождения и коэффициент отражения используются для описания вероятности прохождения и отражения волн падающих на барьер. Коэффициент прохождения представляет собой отношение потоков прошедших частиц к потоку падающих частиц. Он также используется для описания вероятности прохождения через барьер (туннелирование) частиц.
Коэффициент прохождения определяется в терминах падающей и прошедшей токов вероятности j согласно:
где ji — ток вероятности падающей на барьер волны и jt — ток вероятности волны прошедшей барьер.
Коэффициент отражения R определяется аналогично как
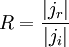 , где jr — ток вероятности волны отражённой от барьера. Сохранения вероятности, а в данном случае оно эквивалентно сохранению числа частиц накладывает условие на коэффициенты прохождения и отражения T + R = 1.
, где jr — ток вероятности волны отражённой от барьера. Сохранения вероятности, а в данном случае оно эквивалентно сохранению числа частиц накладывает условие на коэффициенты прохождения и отражения T + R = 1.Для примера смотрите Туннелирование через прямоугольный барьер или Надбарьерное отражение.
ВКБ приближение
Используя ВКБ приближение можно получить туннельный коэффициент, который записывается в виде
где x1,x2 — две классические точки поворота для потенциального барьера. Если мы возьмём классический предел где все остальные физические параметры много больше постоянной Планка, записанный как
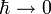 , мы увидим, что коэффициент прохождения стремится к нулю. Этот классические предел нарушается в случае нефизического (в силу непременимости квазиклассического приближения), но более простого случая прямоугольного барьера.
, мы увидим, что коэффициент прохождения стремится к нулю. Этот классические предел нарушается в случае нефизического (в силу непременимости квазиклассического приближения), но более простого случая прямоугольного барьера.Если коэффициент прохождения много меньше 1, формулу можно записать в виде:
где L = x2 − x1 — длина потенциального барьера.
Смотрите также
Туннелирование через дельтообразный потенциал
Ссылки
- Introduction to Quantum Mechanics (2nd ed.). — Prentice Hall, 2004. — ISBN ISBN 0-13-805326-X
-
Wikimedia Foundation. 2010.