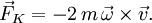- Кориолиса сила
-
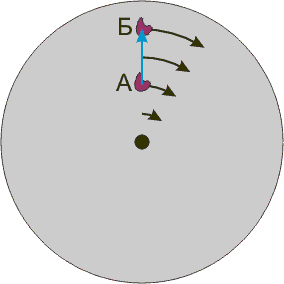 При вращении диска, более далёкие от центра точки движутся с большей касательной скоростью, чем менее далёкие (группа чёрных стрелок вдоль радиуса). Если мы хотим переместить некоторое тело вдоль радиуса, так, чтобы оно оставалось на радиусе (синяя стрелка из положения «А» в положение «Б»), то нам придётся увеличить скорость тела, то есть, придать ему ускорение. Если наша система отсчёта вращается вместе с диском, то мы ощутим, что тело «не хочет» оставаться на радиусе, а «норовит» уйти влево — это и есть сила Кориолиса.
При вращении диска, более далёкие от центра точки движутся с большей касательной скоростью, чем менее далёкие (группа чёрных стрелок вдоль радиуса). Если мы хотим переместить некоторое тело вдоль радиуса, так, чтобы оно оставалось на радиусе (синяя стрелка из положения «А» в положение «Б»), то нам придётся увеличить скорость тела, то есть, придать ему ускорение. Если наша система отсчёта вращается вместе с диском, то мы ощутим, что тело «не хочет» оставаться на радиусе, а «норовит» уйти влево — это и есть сила Кориолиса. Движение шарика по поверхности вращающейся тарелки.
Движение шарика по поверхности вращающейся тарелки.Си́ла Кориоли́са (по имени французского учёного Гюстава Гаспара Кориолиса, впервые его описавшего) — одна из сил инерции, существующая в неинерциальной (вращающейся) системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения. Ускорение Кориолиса было получено Кориолисом в 1833 г., Гауссом в 1803 г. и Эйлером в 1765 г.
Причина появления силы Кориолиса — в кориолисовом (поворотном) ускорении. Для того, чтобы тело двигалось с кориолисовым ускорением, необходимо приложение силы к телу, равной F = ma, где a — кориолисово ускорение. Соответственно, тело действует по третьему закону Ньютона с силой противоположной направленности. FK = − ma. Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другой силой инерции — центробежной силой, которая направлена по радиусу вращающейся окружности.
В инерциальных системах отсчёта действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса.
Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки — то вправо.
Содержание
Математическое определение
Сила Кориолиса равна:
где m — точечная масса,
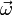 — вектор угловой скорости,
— вектор угловой скорости, 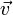 — вектор скорости движения точечной массы.
— вектор скорости движения точечной массы.Кориолисово ускорение — это векторная величина, равная
![\vec{a}_k=2 \left[ \vec \omega \times \vec v \right],](/pictures/wiki/files/55/7b078ba4ad487c59c24ab9381f405b3f.png) где
где 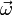 — угловая скорость неинерциальной системы отсчёта относительно инерциальной,
— угловая скорость неинерциальной системы отсчёта относительно инерциальной, 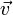 — скорость объекта в неинерциальной системе отсчёта.
— скорость объекта в неинерциальной системе отсчёта.Получение
Пусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта со скоростью
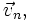 а сама система движется поступательно с линейной скоростью
а сама система движется поступательно с линейной скоростью 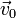 в инерциальной системе координат и одновременно вращается с угловой скоростью
в инерциальной системе координат и одновременно вращается с угловой скоростью 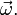
Тогда линейная скорость тела в инерциальной системе координат равна:
![\vec v= \vec {v}_0 + \left[ \vec \omega \times \vec R \right] + \vec {v}_n,](/pictures/wiki/files/100/d3ee4158828c2b1125e1761fd6670ab5.png)
где
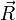 — радиус-вектор центра масс тела относительно неинерциальной системы отсчета. Продифференцируем данное уравнение:
— радиус-вектор центра масс тела относительно неинерциальной системы отсчета. Продифференцируем данное уравнение:![\frac{d}{dt}\vec v= \frac{d}{dt}\vec {v}_0 + \frac{d}{dt}\left[ \vec \omega \times \vec R \right] +\frac{d}{dt} \vec {v}_n.](/pictures/wiki/files/51/3af4b9a812a8b372387d54168f2dba94.png)
Найдём значение каждого слагаемого в инерциальной системе координат:
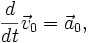
![\frac{d}{dt} \vec {v}_n = \vec {a}_n + \left[ \vec\omega \times \vec {v}_n \right],](/pictures/wiki/files/53/564bf2b000132c2b979c4abe8bbcd2c5.png)
![\frac{d}{dt} \left[ \vec\omega \times \vec R \right] = \left[ \vec \varepsilon \times \vec R \right] + \left[ \vec\omega \times \frac{d}{dt} \vec R \right] = \left[ \vec \varepsilon \times \vec R \right] + \left[ \vec\omega \times \vec {v}_n \right] + \left[ \vec\omega \times \left[ \vec\omega \times \vec R \right] \right],](/pictures/wiki/files/101/e5ef1554861e7cb48ef0e7a990349ddd.png) где
где 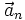 — линейное ускорение относительно системы,
— линейное ускорение относительно системы, 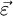 — угловое ускорение.
— угловое ускорение.Таким образом, получаем:
![\frac{d}{dt}\vec v = \vec a=\vec {a}_0 + \vec {a}_n + \left[ \vec \varepsilon \times \vec R \right] + \left[ \vec \omega \times \left[ \vec \omega \times \vec R \right] \right] + 2\left[ \vec \omega \times \vec {v}_n \right].](/pictures/wiki/files/99/cee134148f3010b2696e9e0f94b9b9d3.png) Последнее слагаемое и будет кориолисовым ускорением.
Последнее слагаемое и будет кориолисовым ускорением.Физический смысл
Пусть тело движется со скоростью
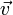 вдоль прямой к центру вращения инерциальной системы отсчёта.
вдоль прямой к центру вращения инерциальной системы отсчёта.Тогда данное движение приведёт к изменению расстояния до центра вращения R и, как следствие, абсолютной скорости движения точки неинерциальной системы отсчёта, совпадающей с движущейся точкой.
Как мы знаем, эта скорость движения равна
![\vec {v}_e = \left[ \vec \omega \times \vec R \right].](/pictures/wiki/files/97/aa9de6f46034488f4bbca755d76bc9f5.png)
Данное изменение будет равно:
![d \vec {v}_e= \left[ \vec\omega \times d \vec R \right].](/pictures/wiki/files/48/0baa1c9caf22087ed731e63f30de4be5.png)
Проведя дифференцирование по времени, получим
![\vec a = \left[ \vec\omega \times \vec v \right]](/pictures/wiki/files/99/c8317f0075818272e2bc3cd7e7b8b78d.png) (направление данного ускорения перпендикулярно
(направление данного ускорения перпендикулярно 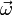 и
и 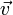 ).
).C другой стороны, вектор
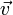 , оставшись неподвижным относительно инерциального пространства, повернётся относительно неинерциального на угол ωdt. Или приращение скорости будет
, оставшись неподвижным относительно инерциального пространства, повернётся относительно неинерциального на угол ωdt. Или приращение скорости будет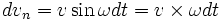 при
при 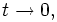 соответственно второе ускорение будет:
соответственно второе ускорение будет:![\vec a= \left[ \vec\omega \times \vec v \right]](/pictures/wiki/files/99/c8317f0075818272e2bc3cd7e7b8b78d.png)
Общее ускорение будет
![\vec {a}_k=2 \left[ \vec\omega \times \vec v \right].](/pictures/wiki/files/50/2852b6463402e829d89a249960f33f2c.png) Как видно, система отсчёта не претерпела изменения угловой скорости
Как видно, система отсчёта не претерпела изменения угловой скорости 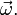 Линейная скорость относительно неё не меняется и остаётся
Линейная скорость относительно неё не меняется и остаётся 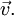 Тем не менее, ускорение не равно нулю.
Тем не менее, ускорение не равно нулю.Если тело движется перпендикулярно направлению к центру вращения, то доказательство будет аналогичным. Ускорение из-за поворота вектора скорости останется
![\vec a = \left[ \vec\omega \times \vec v \right],](/pictures/wiki/files/51/3537afd827222e73c0737864244d6b7b.png) а также прибавляется ускорение в результате изменения центростремительного ускорения точки.
а также прибавляется ускорение в результате изменения центростремительного ускорения точки.Сила Кориолиса в природе
Самый простой пример использования силы Кориолиса — это эффект ускорения кручения танцоров. Чтобы ускорить свое вращение, человек может начать крутиться с широко разведёнными в стороны руками, а затем — уже в процессе — резко прижать руки к туловищу, что вызовет увеличение круговой скорости (согласно закону сохранения момента импульса). Эффект силы Кориолиса проявится в том, что для такого движения руками придётся прикладывать усилия не только по направлению к телу, но и в направлении по вращению. При этом возникает ощущение, что руки отталкиваются от чего-то, при этом ещё больше ускоряясь.
Сила Кориолиса также проявляется, например, в работе маятника Фуко. Кроме того, поскольку Земля вращается, то сила Кориолиса проявляется и в глобальных масштабах. В северном полушарии сила Кориолиса направлена вправо от движения, поэтому правые берега рек в Северном полушарии более крутые — их подмывает вода под действием этой силы (см. Закон Бэра). В Южном полушарии всё происходит наоборот. Сила Кориолиса ответственна также и за вращение циклонов и антициклонов.
Вопреки расхожему мнению, маловероятно, что сила Кориолиса полностью определяет направление закручивания воды в водопроводе — например, при сливе в раковине. Хотя в разных полушариях она действительно стремится закручивать водяную воронку в разных направлениях, при сливе возникают и побочные потоки, зависящие от формы раковины и конфигурации канализационной системы. По абсолютной величине создаваемые этими потоками силы превосходят силу Кориолиса, поэтому направление вращения воронки как в Северном, так и в Южном полушарии может быть как по часовой стрелке, так и против неё.
См. также
Wikimedia Foundation. 2010.