Интерпретация Пуанкаре

Вы читаете самую свежую версию статьи; также доступна выверенная версия.

Замощение плоскости Лобачевского правильными треугольниками.

Конформно-евклидова модель Пуанкаре — модель пространства Лобачевского, предложенная Анри Пуанкаре в 1882 году^[1] в связи с задачами теории функций комплексного переменного. Существуют разновидности модели — в круге и на полуплоскости для планиметрии Лобачевского, а также в шаре и в полупространстве — для стереометрии Лобачевского, соответственно.

Модель Пуанкаре примечательна тем, что в ней углы изображаются обычными углами (то есть модель Пуанкаре конформна)^[2] в отличие от модели Клейна, в которой определение углов производится гораздо сложнее.

Модели Пуанкаре в круге и в шаре

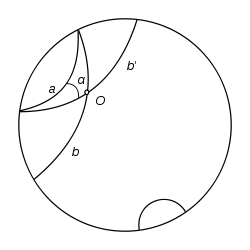Модель Пуанкаре в круге

В модели Пуанкаре в круге за плоскость Лобачевского принимается внутренность круга (изображено на иллюстрации) в евклидовом пространстве; граница данного круга (окружность) называется «абсолютом». Роль прямых выполняют содержащиеся в этом круге дуги окружностей $(a,\;b,\;b')$, перпендикулярных абсолюту, и его диаметры; роль движений — преобразования, получаемые комбинациями инверсий относительно окружностей, дуги которых служат прямыми.

Метрикой ds плоскости Лобачевского в модели Пуанкаре в единичном круге является: 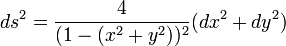$ds^2=\frac{4}{(1-(x^2+y^2))^2}(dx^2+dy^2)$, где x и y — оси абcцисс и ординат, соответственно.^[3]

Аналогично, в модели Пуанкаре в шаре роль абсолюта выполняет граничная сфера в трёхмерном евклидовом пространстве, а пространством Лобачевского является внутренность шара.

Модели Пуанкаре на полуплоскости и в полупространстве

В модели Пуанкаре на полуплоскости за плоскость Лобачевского принимается верхняя полуплоскость. Прямая, ограничивающая полуплоскость (то есть ось абcцисс), называется «абсолютом». Роль прямых выполняют содержащиеся в этой полуплоскости полуокружности с центрами на абсолюте и начинающиеся на абсолюте перпендикулярные ему лучи (то есть вертикальные лучи). Роль движений — преобразования, получаемые композицией конечного числа инверсий с центром на абсолюте и осевых симметрий, оси которых перпендикулярны абсолюту.

Метрика ds плоскости Лобачевского в модели Пуанкаре в верхней полуплоскости имеет вид: $ds^2=\frac{1}{v^2}(du^2+dv^2)$.^[3]

Соответственно, в модели Пуанкаре в полупространстве роль абсолюта выполняет плоскость в трёхмерном евклидовом пространстве, а пространством Лобачевского является лежащее на этой плоскости полупространство.

Ссылки

• Черников Н. А. Преобразование Боголюбова и планиметрия Лобачевского. Раздел 4, сравнение двух моделей Пуанкаре.
• Самаров К., Уроев В. «Модель Пуанкаре». — Журнал «Квант». — 1984 год. — номер 6.

Примечания

1. ↑ Учебник «Открытая математика 2.5. Планиметрия», ООО «Физикон»
2. ↑ Попов А. Г. Псевдосферические поверхности и некоторые задачи математической физики
3. ↑ ^{1 2} Буяло С. В. Курс лекций «Асимптотическая геометрия метрических пространств» весна 2004.