Закон подлости

Зако́н Мёрфи (англ. Murphy's law) — универсальный философский принцип, состоящий в том, что если есть вероятность того, что какая-нибудь неприятность может случиться, то она обязательно произойдёт. Иностранный аналог русского «закона подлости» и «закона бутерброда».

Происхождение

В 1949 г. на базе ВВС США Эдвардс в Калифорнии исследовались причины аварий самолётов. Служивший на базе капитан Эдвард Мёрфи (вар. Мэрфи, англ. Murphy), оценивая работу техников одной из лабораторий, утверждал, что если можно сделать что-либо неправильно, то эти техники именно так и сделают. По легенде, фраза («Если существуют два способа сделать что-либо, причём один из которых ведёт к катастрофе, то кто-нибудь изберёт именно этот способ») впервые была сказана в момент, когда заведённый самолётный двигатель начал вращать пропеллер не в ту сторону. Как потом выяснилось, техники установили детали задом наперёд.

Руководитель проекта от компании Нортроп Дж. Никольс назвал эти постоянные неполадки «законом Мёрфи». На одной из пресс-конференций проводивший её полковник ВВС заявил, что всё достигнутое по обеспечению безопасности полётов является результатом преодоления «закона Мёрфи». Так выражение попало в прессу. В последующие несколько месяцев этот принцип стал широко использоваться в промышленной рекламе и попал в жизнь.

Формулировка

В современной трактовке закон Мёрфи обычно проще всего сформулировать в терминах классической теории вероятностей:

Если проводится n испытаний, результат каждого из которых оценивается логической функцией z, причём результат «ложь» является нежелательным, то для достаточно большого n обязательно хотя бы для одного испытания A получим нежелательный результат $\lnot z(A)$.

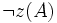Закон Мёрфи подтверждается во всех практических испытаниях. Это в некоторой степени роднит закон Мёрфи с большой теоремой Ферма (последняя была доказана совсем недавно, по прошествии нескольких веков с момента формулировки).

Комментарий Каллагана

Каллаган дал комментарий к закону Мёрфи. Он сформулировал его в форме:

Мёрфи был оптимистом.

Позднее комментарий Каллагана был переформулирован в более строгой форме в виде:

Для любого n найдётся m, причём m < n, такое, что если n достаточно велико для выполнения закона Мёрфи в данных конкретных условиях, то m испытаний достаточно, чтобы хотя бы одно из них A дало нежелательный результат $\lnot z(A)$.

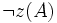Следствия

Следствия из закона Мёрфи были впервые опубликованы в книге Артура Блоха «Закон Мёрфи». Авторство не установлено (скорее всего, не собственно Эда Мёрфи).

Следствия были опубликованы в словесной форме, не лишенной доли юмора. Сегодня эту форму называют «канонической». Все следствия в канонических формулировках следует понимать как имеющие место в условиях закона Мёрфи, то есть для достаточно большого числа испытаний при условии наличия функции, оценивающей желательность или нежелательность отдельного события. С учётом этого разработаны современные строгие формулировки следствий.

Первые пять следствий формулируются, как и сам закон Мёрфи, в терминах теории вероятностей. Шестое и седьмое следствия носят более философский характер.

Первое и второе

Каноническая формулировка:

1. Всё не так легко, как кажется.
2. Всякая работа требует больше времени, чем вы думаете.
3. До поры, до времени.

По сути это один принцип. Его строгая формулировка:

Если имеется оценочная функция, причем желательными значениями являются неотрицательные, и известно, что для n испытаний функция достаточно достоверно даёт неотрицательные значения, то всегда найдётся m < n, такое, что для m испытаний функция обязательно даст весомое количество отрицательных значений.

Третье

Каноническая формулировка: «изо всех возможных неприятностей произойдёт именно та, ущерб от которой больше».

Строгая формулировка:

Если есть несколько возможных вариантов исхода каждого из событий, и часть вариантов является нежелательной, причём в разной степени, то при возрастании количества испытаний вероятность выпадения наиболее нежелательного варианта стремится к единице.

Это следствие является достаточно спорным. Многие учёные считают, что даже если закон Мёрфи будет доказан, третье следствие доказать не удастся; многие учёные полагают, что его удастся опровергнуть (по сей день это сделать, однако, не удалось).

Четвёртое

Каноническая формулировка: «если четыре причины возможных неприятностей заранее устранены, то всегда найдётся пятая».

Строгая формулировка:

Если исход события зависит от бесконечного числа априорных факторов, причём из них найдено n таких, о которых достоверно известно, что их наличие приведёт к нежелательному исходу, то всегда существует (n + 1)-й такой фактор.

Пятое

Каноническая формулировка: «предоставленные сами себе события имеют тенденцию развиваться от плохого к худшему».

Строгая формулировка:

При неограниченном возрастании количества испытаний вероятность нежелательного исхода возрастает (в других формулировках — стремится к единице).

Шестое

Каноническая формулировка: «как только вы принимаетесь делать какую-то работу, находится другая, которую надо сделать ещё раньше».

Строгая формулировка:

Для любого процесса найдётся такой, без завершения которого невозможен данный.

Седьмое

Каноническая формулировка: «всякое решение плодит новые проблемы».

Строгая формулировка:

Устранение факторов, могущих привести к нежелательному исходу, обнаруживает новые такие факторы.

Генеральский эффект

Если испытания системы проводятся перед заказчиком, то она обязательно даст сбой.

Известен также под названием «эффект демонстрации» («визит-эффект»). Он подразумевает невозможность сделать перед зрителями то, что без зрителей делалось без проблем. Чем демонстрирующий сильнее заинтересован в успехе демонстрации, тем сильнее проявляется этот эффект.

Философия

Закон отражает отношение инженеров к жизни. Инженеры знают, что вначале сложную систему испытывают — и она почти наверняка не работает. И не предполагается, что она сразу будет работать. Цель испытаний — определить несовершенство в системе, чтобы его можно было устранить. Есть принципиальное различие между тем, как подходит к этому закону инженер и обычный человек.

См. также

• Бритва Хэнлона

Ссылки

• Законы Мёрфи