- Еггог
-
 Электроника МК-52 с сообщением "ERROR" (из-за специфического отображения буквы r зачастую читалось как «ЕГГОГ»
Электроника МК-52 с сообщением "ERROR" (из-за специфического отображения буквы r зачастую читалось как «ЕГГОГ»Еггоголо́гия — изучение скрытых возможностей микрокалькуляторов.
Происхождение
Название происходит от сообщения об ошибке «ЕГГОГ» (англ. Error — ошибка), которую выдавали отечественные программируемые микрокалькуляторы второго поколения (Электроника Б3-34, МК-54, МК-56, МК-61, МК-52). Термин впервые появился в журнале «Техника — молодёжи» после цикла статей, посвященных программированию на микрокалькуляторах серии «Электроника Б3-34»[1] и серии из девяти рассказов об увлекательном фантастическом путешествим с Луны на Землю (автор — Михаил Пухов) под общим названием «„Кон-Тики“: путь к Земле»[2]. В этом цикле, кроме игровых программ, описывались различные недокументированные возможности микрокалькуляторов и видеосообщения, многие из которых получались путем манипуляций с клавишами после появления сообщения об ошибке «ЕГГОГ» (
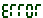 ).
).Читатели журнала с огромным энтузиазмом откликнулись на рассказ об обнаруженных недокументированных возможностях микрокалькуляторов, стали искать новые, и по окончанию цикла «Кон-Тики…» появился небольшой раздел «Новости еггогологии». С помощью опубликованных в нём недокументированных приёмов было написано множество новых игровых программ, большинство из которых просто не могло быть создано стандартными средствами, в силу ограниченности ресурсов калькуляторов семейства Б3-34.
Направления еггогологии
Одним из основных направлений еггогологии было расширение диапазона обрабатываемых чисел, и изучение реакции микрокалькулятора на попытки произвести операции с числами за пределами стандартного диапазона.
Другое направление еггогологии изучало реакцию микрокалькулятора на недокументированные последовательности нажатия программных клавиш и способы ввода недокументированных команд, а также исполнение микрокалькуляторами таких команд.
«Нестандартные» числа
Еггогология утверждает, что порядок (показатель степени) диапазона обрабатываемых микрокалькулятором чисел ограничено по модулю 1000 и делит этот диапазон на так называемые этажи или «ярусы»[3]. Каждый ярус — это сотня из диапазона от 0 до 999. То есть нулевой ярус — это числа с основанием степени от 0 до 99, первый ярус — числа с основанием степени от 100 до 199 и т. д. Всего ярусов десять, причем минус первый ярус эквивалентен девятому (то есть основание степени −80 в представлении микрокалькулятора эквивалентно основанию степени 920), минус второй — восьмому (например −180 эквивалентно 820) и т. д.
Документацией максимальное значение чисел, над которыми можно производить математические действия, ограничивалось значением ±9.9999999 × 10±99 (то есть нулевым и минус первым ярусами). В самом деле, если ввести в микрокалькулятор число 1 × 1050 (для чего достаточно последовательности нажатий клавиш 1 ВП 50) и возвести его в квадрат (нажать Fx²), то получаем сообщение на дисплее «ЕГГОГ». Такая индикация по документации является признаком сообщения об ошибке, так как число 1 × 10100 выходит за пределы «стандартного» диапазона. Оказывается, что это не сообщение об ошибке, а способ индикации чисел первого яруса, и с этим числом можно производить обычные операции: складывать, умножать, делить, вычислять значения функций, запоминать его в регистре памяти, вызывать из регистра. Таким же образом можно работать с числами второго яруса (например 1 × 10200, простейший способ получить такое число — возвести в квадрат число 1 × 10100). Чтобы выяснить реальные значения таких чисел, их нужно было разделить на 1 × 1099 или другие подобные числа для приведения к числу из нулевого яруса (по абсолютному модулю не более 9.9999999 × 1099).
Другими словами, давался способ расширения диапазона чисел, обрабатываемых стандартными действиями, до ±9.9999999 × 10299. Также было возможно с некоторыми ухищрениями (с помощью специально написанных программ) получать числа до ±9.9999999 × 10799 и анализировать их значение (то есть выяснить мантиссу и порядок). С помощью таких «вычислений» доказывалось, что девятый ярус представляет собой числа с отрицательным значением основания степени (например, 1 × 10920 было эквивалентным представлением числа 1 × 10-80). Числа восьмого яруса (числа от ±1 × 10800 до ±9.9999999 × 10899 а также от ±1 × 10900 до ±9.9999999 × 10900) невозможно сохранить после их получения, так как они немедленно преобразовывались в обычный нуль, независимо от того, с какой стороны к ним «подбираться» (с седьмого или девятого яруса).
Классификация числовых ярусов
Числовой ярус Название чисел Диапазон чисел Краткая характеристика числа из этого диапазона Нулевой Обычные числа с неотрицательным порядком От ±1 до ±9.9999999 × 1099 Можно производить обычные вычисления Первый «ЕГГОГи» От ±1 × 10100 до ±9.9999999 × 10199 Можно производить обычные вычисления, но отображаются на дисплее как 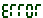
Второй «3ГГОГи» От ±1 × 10200 до ±9.9999999 × 10299 Можно производить обычные вычисления, но отображаются на дисплее как 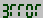 . Выполняют безусловный переход на адрес, совпадающий с двумя первыми цифрами порядка (от 20 до 29)
. Выполняют безусловный переход на адрес, совпадающий с двумя первыми цифрами порядка (от 20 до 29)Третий «Неукротимые чудовища» От ±1 × 10300 до ±9.9999999 × 10399 Способны произвольно перевести микрокалькулятор в режим исполнения программы или привести к его зависанию Четвертый «ОС-оборотни» От ±1 × 10400 до ±9.9999999 × 10499 Копируют в искажённом виде структуру ярусов, применяются для анализа других чисел. Искажают содержимое регистра С Пятый «Тьма» От ±1 × 10500 до ±9.9999999 × 10599 При попытке вывода на дисплей приводят к зависанию микрокалькулятора. Индикатор гаснет, работоспособность восстанавливается после выключения и включения Шестой «С-ЕГГОГ-оборотни» От ±1 × 10600 до ±9.9999999 × 10699 Искажают содержимое регистра С Седьмой «Длинные монстры» От ±1 × 10700 до ±9.9999999 × 10799 Копируют в искажённом виде структуру ярусов, применяются для анализа других чисел Восьмой (минус второй) «Нули» От ±1 × 10800 до ±9.9999999 × 10900 или от ±1 × 10-200 до ±9.9999999 × 10-100 (зависит от способа получения) Немедленно преобразовывается в обычный ноль Девятый (минус первый) Обычные числа с отрицательным порядком От ±1 × 10-99 до ±9.9999999 × 10-1 Можно производить обычные вычисления Подробное описание
«ОС-оборотни»
От ±1 × 10400 до ±9.9999999 × 10499
При вытаскивании «ОС-оборотня» из регистра он заносит свой «хвост» в регистр С. «Хвост» также является сверхчислом, чьи две первые цифры порядка являются последними двумя цифрами порядка «ОС-оборотня». Если «хвост» также является «ОС-оборотнем» (это происходит для чисел с порядками с 440 по 449), то он также заносит свой «хвост» в регистр С. Существуют оборотни 3-го порядка - числа с порядком 444.
Пример:
В/О FПРГ Fx2 Fx2 × Fx2 ХПС Сх С/П FАВТ В/О 1 ВП 22 В↑ 1 ВП 50 С/П
ПХС на экране 0
ПХС на экране 0
ПХС на экране 0
ПХС на экране последний «Хвост» с тремя буквами Е.«С-ЕГГОГ-оборотни»
От ±1 × 10600 до ±9.9999999 × 10699
Если «С-ЕГГОГ-оборотня» вытащить из регистра, то он прикроется содержимым регистра C, а сам переместится в регистр Y. При выполнении над ним арифметической операции - Г.ГГОГ
На основе свойств «С-ЕГГОГ-оборотня» придуман т.н. «АСО-анализ»:- В регистр 0 помещаем "С-ЕГГОГ-оборотень" (можно и в другой регистр)
- В регистр А (только!) помещаем ЕГГОГ.
- ПXA ПX0 PX - содержимое регистра C - мантисса и 3-х значная степень
- /-/ - содержимое P0
Меры предосторожности при работе с «С-ЕГГОГ-оборотнями»:
- «Тьма» наступает:
- если после «АСО-анализа» нажать ВП, FАВТ
- если сразу после формирования ЕГГОГА вытащить «С-ЕГГОГ-оборотня»
- если вытащить «С-ЕГГОГ-оборотня» при «ПСЧ-режиме»
- если «С-ЕГГОГ-оборотень» вытаскивает из регистра C сам себя
«Длинные монстры»
Другое название — «К-числа»
От ±1 × 10700 до ±9.9999999 × 10799
На индикаторе при появлении «Длинного монстра» появляется следующее число:
1,2345678*10735 = [50.12345678 3] Где первая цифра 5 на индикаторе это третья цифра порядка, а последняя цифра 3 на индикаторе это вторая цифра порядка. А сам «Длинный монстр» записывается на 73 адрес программы, что соответствует первым двум цифрам порядка числа.Недокументированные команды
Команды «со стре́лками» в Б3-34
На микрокалькуляторе Б3-34 (и совместимых с ним МК-54, МК-56) существуют недокументированные команды КИП↑, КП↑ и др., которые обеспечивают косвенный доступ к регистру 0, но, в отличие от соответствующих команд КИП0, КП0 и др., не уменьшают его значения. Этот способ использования регистра 0 в некоторых случаях упрощал вычисления в программах. На микрокалькуляторах МК-61 и МК-52 такая команда не работает, так как в архитектуре МК-61/52 добавлен регистр Е, и коды недокументированных команд Б3-34 «со стрелками» совпадают с кодами соответствующих документированных команд МК-61/52 для косвенного доступа к регистру Е[4] (см. табл.). Заметим, что обозначениям клавиш в Б3-34 П, ИП и ↑ соответствуют Х→П, П→Х и Е в МК-61 и МК-52.
Коды команд Команды Б3-34 Команды МК-61, МК-52 7E Kx≠0↑ Kx≠0E 8E КБП↑ КБПЕ 9E Kx≥0↑ Kx≥0E -E КПП↑ КППЕ LE КП↑ КX→ПЕ CE Кх<0↑ Kx<0E ГE КИП↑ КП→ХЕ EE Kx=0↑ Kx=0E Некорректные операции с клавишей К
На микрокалькуляторе Б3-34 большинство недокументированных операций с клавишей К вызывает сообщение ЕГГОГ. Это команды К3—К9, К+, К−, К×, К÷, КХ↔У, К↑, К/−/, КВП, КСх и К десятичная запятая. Команды К1 и К2 эквивалентны операции КНОП.
На МК-61 и МК-52 к сообщению ЕГГОГ приводят только команды К−, К×, К÷. Команды К1 и К2 также эквивалентны операции КНОП. Коды остальных команд документированы и используются для преобразования временны́х и угловых мер, определения модуля и знака числа, целой и дробной частей числа, бо́льшего из двух чисел, логических операций и генерации случайного числа.
Сообщение ЕГГОГ, полученное с помощью недокументированных операций с клавишей К, не является «сверхчислом» первого «яруса» и не может быть сохранено в регистре памяти, но может быть использовано для вывода на индикатор символов 16-ричных цифр, например:
1 К− (высвечивается ЕГГОГ) ВП ВП ↑ (высвечивается буква Е).
Полученную букву Е можно сохранять в регистрах памяти и извлекать оттуда, а с помощью регистров 0—3 также и преобразовывать в символы других 16-ричных цифр:
П0 КИП0 ИП0 КНОП (Г) КИП0 ИП0 КНОП (С) КИП0 ИП0 КНОП (L) КИП0 ИП0 КНОП (-) КИП0 ИП0 КНОП (9) и т.д.
Подобные приёмы использовались для формирования видеосообщений, например, в игровых программах.
Получение видеосообщения, начинающегося с цифры F (изображается как пустое место) может нарушить нормальную работу микрокалькулятора (искажение программы и данных, самопроизвольный переход в режим счёта и т.п.). Избежать этого можно, сразу же «изгнав» его командой ↑, подаваемой не менее четырёх раз[4] (по другим данным — семь раз[5]),не пытаясь проводить какие-либо другие операции.
Искусственный ввод кодов команд
В одном шаге программной памяти микрокалькулятора могут содержаться две шестнадцатеричные цифры, т.е. теоретически может существовать 256 различных кодов команд. Из них в руководстве пользователя МК-61/52 документированы 214. Существует искусственный приём, позволяющий ввести 12 из 42 недокументированных кодов. Для этого вводится одна из команд переходов, например БП (код 51) и за ней две 16-ричные цифры, воспринимаемые калькулятором как адрес перехода. После этого команда перехода затирается командой-«пустышкой» КНОП, а последующий шаг при выполнении программы будет воспринят калькулятором уже не как адрес перехода, а как команда[6]. Отметим, что некоторые из этих кодов можно ввести также путём недокументированных операций с клавишей К, описанных в предыдущем подразделе.
Коды команд Действия команд Ввод через клавишу К 27 Вызывает сообщение ЕГГОГ K− 28 Вызывает сообщение ЕГГОГ К× 29 Вызывает сообщение ЕГГОГ K÷ 2L Вызывает сообщение ЕГГОГ Нет 2С Вызывает сообщение ЕГГОГ Нет 2Г Вызывает сообщение ЕГГОГ Нет 2E Вызывает сообщение ЕГГОГ Нет 3С Вызывает сообщение ЕГГОГ Нет 3Г Ничего не делает (?) По другим сведениям — копирует содержимое регистра Х в Х1 Нет 3Е Перемещает содержимое регистра Х в Х1, копирует содержимое регистра Y в Х. Содержимое регистров Y, Z и Т сохраняется.
Нет 55 Ничего не делает (равнозначна команде КНОП) К1 56 Ничего не делает (равнозначна команде КНОП) К2 Коды 55 и 56 использовались во входных языках малосерийных аналогов МК-52.[7]
Данный приём неприменим для ввода остальных 30 недокументированных кодов команд, содержащих 16-ричную цифру F (изображаемую на индикаторе как пустое знакоместо), поскольку на клавиатуре микрокалькулятора нет клавиши для ввода цифры F (не путать с префиксной клавишей F). Некоторые способы ввода таких кодов будут рассмотрены в следующем подразделе.
Ввод кодов команд, содержащих цифру F
В микрокалькуляторе МК-52 существует возможность формирования любого из 256 кодов команд по любому из адресов программной памяти. Для этого используется следующая особенность записи программ в ППЗУ. При нормальном процессе записи программы необходимо сначала стереть соответствующий участок памяти ППЗУ. Если же этого не сделать, то происходит побитовое логическое сложение кодов команд из ОЗУ с кодами, имевшимися в ППЗУ ранее[8]. Так, если в ППЗУ по некоторому адресу записана команда БП (код 51), а по соответствующему адресу в ОЗУ находится команда В↑ (код 0Е), то результатом логического сложения будет команда с кодом 5F (которая приводит к зависанию микрокалькулятора). Действия команд с кодами, содержащими цифру F, приведены в следующей таблице:
Коды команд Действия команд 0F Документированная команда FBx 1F, 2F, 3F Ничего не делают (равнозначны команде КНОП) 4F Равнозначна команде X→П0 (код 40) 5F Приводит к зависанию микрокалькулятора. Индикатор гаснет, работоспособность восстанавливается после отключения и включения питания. 6F Равнозначна команде П→Х0 (код 60) 7F Равнозначна команде Кх≠00 (код 70) 8F Равнозначна команде КБП0 (код 80) 9F Равнозначна команде Кх≥00 (код 90) -F Равнозначна команде КПП0 (код -0) LF Равнозначна команде КХ→П0 (код L0) CF Равнозначна команде Кх<00 (код С0) ГF Равнозначна команде КП→Х0 (код Г0) EF Равнозначна команде Кх=00 (код Е0) F0, F1, ... FF Ничего не делают (равнозначны команде КНОП) К сожалению, недокументированные команды 7F, 8F, ... EF, осуществляющие косвенный доступ к регистру 0, уменьшают его содержимое, так же как и их документированные аналоги с кодами 70, 80, ... Е0 и не могут служить заменой командам «со стрелками» в Б3-34.
В Б3-34 и МК-61, не имеющих ППЗУ, также существует возможность ввода некоторых команд с кодами, содержащими цифру F, но лишь по нескольким фиксированным адресам. Один способ состоит в использовании команд В/0 КППN в режиме ручных вычислений (F АВТ), N — любой из регистров (0—9, А—Е). При этом микрокалькулятор переходит в режим програмирования и вставляет код FN по адресу 30+N (для буквенных регистров А—Е соответственно 40—44). Заметим, что при использовании регистров 0—6 результат зависит от их содержимого [9] Другой способ (проверенный его автором только на МК-61[6]) использует воздействие некорректной операции «ВП десятичная запятая» на «сверхчисла» первого «яруса» (ЕГГОГи). Для этого сначала создаётся «сверхчисло» двукратным применением команды ВП с суммой порядков более 99 (например, ВП 10 ВП 90), а затем, после появления сигнала ЕГГОГ, нажатием клавиш «ВП десятичная запятая 0». Это также переводит микрокалькулятор в режим программирования, и в данном примере по адресу 51 будет записана команда F1. Второй знак и адреса, и команды определяется первым знаком порядка в первой команде ВП (например, ВП 20 ВП 80 ВП .0 даёт команду F2 по адресу 52 и т.д.)
Недокументированное применение десятичной запятой в программе
Команда «десятичная запятая» (код 0-), использованная в программе (за исключением случаев документированного применения — для ввода числа по программе знак за знаком), заменяет значение в регистре Х на то, которое было в нём после последней из команд 0, 1, ... 9, В↑, П→Х0, П→Х1, ... П→Х9, П→ХА, ... П→ХЕ. [10]
Недокументированные способы диагностики ошибок
При возникновении сигнала ЕГГОГ при счёте по программе существует два недокументированных способа определить, в результате какой операции произошёл останов[4]:
- Нажатие клавиши ↑ в Б3-34 (В↑ в МК-61/52). Если на индикаторе по-прежнему ЕГГОГ, то произошло переполнение, а если число — некорректная операция, «виновником» которой является это число.
- Нажатие клавиши ВП. Возможные показания индикатора и соответствующие им ошибки:
- «ЕГГОГ 00» — переполнение («сверхчисло» первого «яруса»)
- «Г.ГГОГ 00» — деление на нуль, вычисление логарифма от нуля, степенной функции 00, некорректная операция с клавишей К.
- «ЕГ.ГОГ 00» — вычисление tg 90°.
- «Е.ГГОГ 00» — вычисление арксинуса или арккосинуса от числа, большего 1.
- «ЕГГОГ 00» (с десятичной запятой на том же месте, что в аргументе) — положительный аргумент показательной функции больше допустимого
- «−ЕГГОГ 00» (с десятичной запятой на том же месте, что в аргументе) — отрицательный аргумент показательной функции по модулю больше допустимого, или извлечение квадратного корня из отрицательного числа.
Второй способ не работает после первого, и наоборот. Чтобы применить обе диагностики, необходимо дважды запустить программу с одинаковыми исходными данными.
(В режиме ручных вычислений это также работает, но обычно не требуется, поскольку и так ясно, в результате какой операции возникла ошибка.)
Команда В/0 вне подпрограммы
Команда В/0, предназначенная для завершения подпрограмм, при использовании в основной программе, как правило, осуществляет переход на адрес 01. Этим иногда пользуются для сокращения программы, заменяя две команды БП 01 одной В/0. Особенно часто эта особенность используется при нестандартном использовании адресного пространства программы (см. Главная и побочные ветви). Однако иногда использование этой особенности приводит к неправильному результату.
Причина этой особенности в том, что адреса, с которых вызываются подпрограммы, записываются в пятирегистровый стек возврата, а по команде В/0 извлекаются из него и происходит возврат на адрес, на единицу больший. Если в стек возврата ничего не было записано, в нём хранятся нули и по команде В/0 происходит переход на адрес 01. То же самое произойдёт, если в стек возврата заносилось не более четырёх адресов при вызовах подпрограмм и все они были извлечены при возвратах — следующий извлекаемый адрес будет нулём.
Однако если в стек возврата занесено пять адресов, при извлечении первого из них в последнем регистре формируется «адрес-диверсант», обе цифры которого совпадают с последней цифрой адреса, находившегося там ранее. По мере извлечения остальных адресов из стека возврата, «адрес-диверсант» заполняет все его регистры, и затем, в случае использования команды В/0 вне подпрограммы, переход будет осуществлён неправильно. [4]
Очистить стек возврата можно с помощью ЗГГОГа с нулевой мантиссой: Сх В↑ ÷ ВП Fх2 Сх ↔ Сх
Косвенное обращение к регистру, содержащему число вне допустимого диапазона
Если в каком-либо из регистров 7—Е находится число, по модулю меньшее единицы, то при косвенном обращении к нему формируется адрес перехода, определяемый мантиссой и последней цифрой порядка[4] (см. табл., МN — N-я цифра мантиссы)
Последняя цифра порядка Адрес перехода 1 М7М8 2 М7М8 3 М7М8 4 М6М7 5 М5М6 6 М4М5 7 М2М3 8 М2М3 9 М1М2 0 0М1 ПСЧ-режим
«Псевдосчётный режим» — методика формирования на экране микрокалькулятора произвольных буквенно-цифровых комбинаций, т. н. «слов». Основан на переводе ПМК в особый режим работы, в котором происходит считывание на индикатор записанных в программной памяти кодов (вернее, их первых символов). Описан в заметке «Новости еггогологии» «Техники — молодежи» № 6 за 1987 год[11]. В этой статье первооткрывателями ПСЧ-режима названы С. Банников, И. Емельянов, В. Мурадов. Также приведены альтернативные названия режима — «ненормальный», «режим сбора».
Перед вводом ПМК в ПСЧ-режим в память записывается короткая программа, коды команд которой начинаются со всех возможных символов (для удобства обычно используются сдвоенные символы вида 00, 11, … , EE).
Непосредственно вход в ПСЧ-режим осуществляется выдачей команд 6 F10x K- ВП . 0 В/О В/О БП В/О. Данная процедура по сути представляет собой способ получения команды «пусто-пусто». Также существует возможность входа в ПСЧ-режим из области «длинных монстров».
В ПСЧ-режиме меняются значения клавиш. В/О и Б/П служат теперь для переключения из автономного режима в программный и наоборот. Команды FПРГ и FАВТ, а также любое «сверхчисло» возвращают ПМК в нормальный режим работы. Клавиши ШГ дают возможность перемещаться вдоль записанной в память программы. Клавиши БП и ПП переносят точку просмотра и считывания на 10 адресов вглубь программы, а также позволяют оперировать с числом на индикаторе непосредственно кодами команд.
Клавиша ВП считывает в первый регистр индикатора символ из текущего адреса программной памяти. Формирование «слов» начинается с заготовки вида 11111111, из соответствующей ячейки программной памяти считывается нужный символ, а затем с помощью команд ВП /-/ 1 ПА КИПА ИПА от заготовки отбрасывается последний регистр, а на место первого записывается ноль, который с помощью команды ВП может быть заменен следующим символом.
Метод позволяет вводить в буквенно-цифровые комбинации и пробел (пустышку). Пробел считывается из любого адреса «темной зоны». Однако из-за особенностей работы ПМК после появления «пустышки» при этом необходимы дополнительные действия (прочистка стека, усложненная последовательность команд для укорочения заготовки, соблюдение ограничений на использование клавиш ШГ).Недокументированные особенности команды ВП
Команда ВП превращает 0 в 1. Это используется в программе вычисления факториала для её сокращения, заменяя три команды Fx=0 03 1 одной ВП. [12]
Ошибки в микрокалькуляторах
Кроме недокументированных возможностей, некоторые микрокалькуляторы содержали ошибки.
Ошибки в Б3-21 некоторых выпусков
В первых выпусках микрокалькулятора Б3-21 возникала ошибка при сложении числа, содержащего семь девяток в мантиссе и цифру более 4 в восьмом (неиндицируемом) разряде мантиссы, с бо́льшим по порядку числом; например, при сложении 9,9999999 и 10 получалось 120.
Также в некоторых Б3-21 при вычислении сложных операций (например, синуса) могло исказиться содержимое одного из регистров кольцевого стека.
Некоторые Б3-21 неправильно выполняли оператор вызова подпрограммы ПП, если он находился по одному из адресов 55, 65, 70, 80, 91 или 92. Вместо перехода к подпрограмме в них выполнялся оператор, код которого равен адресу подпрограммы. [13]
Ошибки в Б3-34 некоторых выпусков
В некоторых микрокалькуляторах Б3-34 операция возведения в степень Fxy выполнялась с ошибкой, если предыдущая операция была двухместной (кроме возведения в степень) и в её результате получилось число, имеющее в восьмом разряде мантиссы цифру 5 или 7. Этой ошибки можно избежать, если перед выполнением операции Fxy нажать дополнительно клавиши F1/x F1/x [14] (что заменяет результат двухместной операции таким же результатом одноместной, на котором эта ошибка не возникает). Другие «взаимоисключающие» операции (например, Fx2 F√ или Feх Fln) для этой цели менее пригодны, так как могут привести к переполнению.
В ранних выпусках микрокалькуляторов нельзя было заканчивать подпрограмму командами одноместных операций Fsin, Flg, F√ и др., а также производить смену знака результата вычислений клавишей /−/ [15]
Ошибки в МК-61 и МК-52
Операция Kmax в МК-61 и МК-52 считает нуль самым большим числом. Эта ошибка использовалась в некоторых программах [16]
При некоторых операциях, например, определении дробной части отрицательного числа, возникает «отрицательный нуль» (изображается на индикаторе как «−0»), который при условных переходах ведёт себя как отрицательное число. [17]
Ошибки и нерациональные решения в блоках расширения памяти БРП-3 и БРП-4
В блоке БРП-3, программе 16 использована неправильная формула za = ealnz вместо za = ealnz, соответственно неправильно составлена и программа. Там же для определения аргумента комплексного числа a + bi используется формула φ = arctg(b / a) без учёта как знаков a и b, так и того, что действительная часть может быть нулём. В результате при a < 0 происходит ошибка в определении аргумента на 180°, а при a = 0 — останов деления на ноль.[18]
В блоке БРП-4 в «лунолётной» игровой программе «Космическая посадка» физическая модель совершенно ошибочна, что может приводить к бессмысленным результатам. Например, при свободном падении космического аппарата на Луну с большой высоты глубина кратера может составлять менее 8 мм, хотя скорость в момент соприкосновения с лунной поверхностью превышает 3000 м/с. В том же блоке микрокалькулятор «нарушает правила» в игровых программах «Жизнь» и «Магараджа». Целый ряд программ составлен нерационально и поддаётся значительным сокращениям. Например, программа для отыскания минимальной поверхности Smin или минимальной длины сварных швов Lmin цилиндрической банки заданного объёма V может быть сокращена на 15 шагов при использовании более простых формул.[19]
См. также
Примечания
- ↑ «Техника — молодёжи», 1985, № 1—4, 6.
- ↑ Михаил Пухов. «Кон-Тики»: путь к Земле. — «Техника — молодёжи», 1985, № 8—12; 1986, № 1—4.
- ↑ «Техника — молодёжи», 1986, № 1, с. 54.
- ↑ 1 2 3 4 5 Школа начинающего программиста. Занятие двадцать шестое. — «Наука и жизнь», 1989, № 11, с. 124—130
- ↑ Сергей Фролов. Электроника Б3-34: микрокалькулятор-загадка. Часть 5. — http://www.geocities.com/lautenaus/b334_5.htm
- ↑ 1 2 Alfred Klomp. Some experiments with hacking the ЭЛЕКТРОНИКА МК-61. — http://www.alfredklomp.com/technology/mk-61/
- ↑ Программируемые микрокалькуляторы: устройство и пользование / Под ред. Я. К. Трохименко. — М.: Радио и связь, 1990. — c. 123—124
- ↑ Школа начинающего программиста. Занятие двадцать второе. — «Наука и жизнь», 1989, № 1, с. 124—129.
- ↑ «Техника — молодёжи», 1986, № 5, с. 52.
- ↑ «Наука и жизнь», 1989, № 4, с. 112.
- ↑ http://www.emulator3000.emuita.it/Books/TM/1987_06.djvu
- ↑ Л. М. Финк. Папа, мама, я и микрокалькулятор. — 19??. — с.??
- ↑ Сергей Фролов. История советских калькуляторов. Часть II. — iNFUSED BYTES OnLine, http://www.enlight.spb.ru/ib/also/calcs/calcs2.htm
- ↑ «Наука и жизнь», 1984, № 2, с. 66.
- ↑ В. П. Дьяконов. Справочник по расчётам на микрокалькуляторах. 3-е изд., доп. и перераб. — М.: Наука, Гл. ред. физ.-мат. лит., 1989. — с. 41.
- ↑ «Наука и жизнь», 1988, № 11, с. 84-85
- ↑ «Наука и жизнь», 1988, № 11, с. 84
- ↑ «Наука и жизнь», 19??, № ??
- ↑ «Наука и жизнь», 1991, № 6, с. 130—131.
Ссылки
- Сергей Фролов Электроника Б3-34: микрокалькулятор-загадка. Sergei Frolov's home page. Проверено 18 сентября 2008.
- Игры для ПМК. Lord_BSS project. Проверено 18 сентября 2008.
- Сергей Фролов История советских калькуляторов. Часть II. iNFUSED BYTES OnLine. Проверено 18 сентября 2008.
Wikimedia Foundation. 2010.
