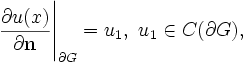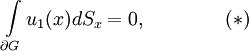Граничные условия второго рода
- Граничные условия второго рода
-
Зада́ча Не́ймана — в дифференциальных уравнениях краевая задача с заданными граничными условиями для производной искомой функции на границе области — так называемые граничные условия второго рода. По типу области задачи Неймана можно разделить на два типа: внутренние и внешние.
Внутренняя задача Неймана
Внутренняя задача Неймана заключается в нахождении гармонической в ограниченной области G функции u, 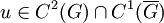 , и удовлетворяющей на границе области G следующему краевому условию:
, и удовлетворяющей на границе области G следующему краевому условию:
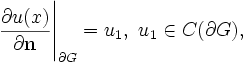
где n — внешняя единичная нормаль к границе области G.
Из теории потенциала известно, что необходимым условием разрешимости внутренней задачи Неймана является выполнение равенства
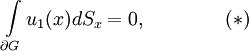
при этом решение внутренней задачи Неймана может быть найдено лишь с точностью до константы.
Внешняя задача Неймана
На неограниченных областях G в постановке задачи Неймана добавляется дополнительное условие ограниченности на бесконечности искомой функции u. Решение внешней задачи Неймана в пространстве размерности n>2 единственно, если на бесконечности функция u→0. В двумерном случае решение может быть найдено с точностью до константы, если выполняется условие (*).
См. также
Литература
В.М. Уроев. Уравнения математической физики. — М.: ИФ Яуза, 1998. — ISBN 5-88923-026-3
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Граничные условия второго рода" в других словарях:
Задача Неймана — Задача Неймана, вторая краевая задача в дифференциальных уравнениях краевая задача с заданными граничными условиями для производной искомой функции на границе области так называемые граничные условия второго рода. По типу области… … Википедия
Уравнение Лапласа — Уравнение Лапласа дифференциальное уравнение в частных производных. В трёхмерном пространстве уравнение Лапласа записывается так: и является частным случаем уравнения Гельмгольца. Уравнение рассматривают также в двумерном и одномерном… … Википедия
Лапласа уравнение — Уравнение Лапласа уравнение в частных производных. В трёхмерном пространстве уравнение Лапласа записывается так: и является частным случаем уравнения Гельмгольца. Уравнение рассматривают также в двумерном и одномерном пространстве. В двумерном… … Википедия
КОНФОРМНОЕ ОТОБРАЖЕНИЕ — непрерывное отображение, сохраняющее форму бесконечно малых фигур. Основные понятия. Непрерывное отображение w=f(z)области G n мерного евклидова пространства в n мерное евклидово пространство наз. конформным в точке если оно в этой точке обладает … Математическая энциклопедия
ЭЛЕКТРОДИНАМИКА — классическая, теория (неквантовая) поведения электромагнитного поля, осуществляющего взаимодействие между электрич. зарядами (электромагнитное взаимодействие). Законы классич. макроскопич. Э. сформулированы в Максвелла уравнениях, к рые позволяют … Физическая энциклопедия
Принцип максимума (уравнение теплопроводности) — Механика сплошных сред Сплошная среда Классическая механика Закон сохранения массы · Закон сохранения импульса … Википедия
Одномерное стационарное уравнение Шрёдингера — Одномерное стационарное уравнение Шрёдингера линейное обыкновенное дифференциальное уравнение второго порядка вида где постоянная Планка, масса частицы, потенциальная энергия, полная энергия … Википедия
Одномерное стационарное уравнение Шредингера — Одномерное стационарное уравнение Шрёдингера линейное обыкновенное дифференциальное уравнение второго порядка вида где постоянная Планка, масса частицы, потенциальная энергия, полная энергия … Википедия
Физика — I. Предмет и структура физики Ф. – наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, свойства и строение материи и законы её движения. Поэтому понятия Ф. и сё законы лежат в основе всего… … Большая советская энциклопедия
МАКРОКИНЕТИКА — (от греч. makros большой и kinetikos приводящий в движение), изучает кинетич. закономерности хим. р ций, к рые сопровождаются одновременно протекающими в системе процессами переноса в ва, энергии, электрич. заряда, импульса. В более узком… … Химическая энциклопедия
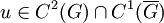 , и удовлетворяющей на границе области G следующему краевому условию:
, и удовлетворяющей на границе области G следующему краевому условию: