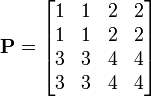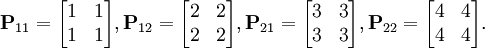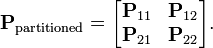Блочнодиагональная матрица

Блочная (клеточная) матрица — вид квадратной матрицы, каждый элемент которой является квадратной подматрицей меньшей, кратной размерности.

Пример записи

Матрица размерностью 4×4

$\mathbf{P} = \begin{bmatrix} 1 & 1 & 2 & 2\\ 1 & 1 & 2 & 2\\ 3 & 3 & 4 & 4\\ 3 & 3 & 4 & 4\end{bmatrix}$

является блочной, состоящей из четырех подматриц-блоков размерностью 2×2

Если каждый блок будет определен как

$\mathbf{P}_{11} = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix}, \mathbf{P}_{12} = \begin{bmatrix} 2 & 2\\ 2 & 2\end{bmatrix}, \mathbf{P}_{21} = \begin{bmatrix} 3 & 3 \\ 3 & 3 \end{bmatrix}, \mathbf{P}_{22} = \begin{bmatrix} 4 & 4\\ 4 & 4\end{bmatrix}.$

то, блочная матрица может быть записана в следующем виде

$\mathbf{P}_{\mathrm{partitioned}} = \begin{bmatrix} \mathbf{P}_{11} & \mathbf{P}_{12}\\ \mathbf{P}_{21} & \mathbf{P}_{22}\end{bmatrix}.$

Операции с блочными матрицами

1. При сложении блочных матриц нужно, чтобы подматрицы были одного размера.
2. При умножении блочной матрицы на число a каждая подматрица умножается на a.
3. При перемножении блочных матриц необходимо согласовать размеры подматриц.
4. При транспонировании блоки на главной диагонали транспонируются и остаются на месте, остальные блоки меняются местами и транспонируются.

Виды блочных матриц

Многие виды матриц могут быть представлены в блочном виде. В этом случае к названию добавляется приставка блочно- или блочная, а операции над элементами трансформируются в операции над блоками.

Блочно-диагональная (квазидиагональная) матрица

У блочно-диагональной матрицы, все подматрицы, кроме расположенных на главной диагонали являются нулевыми.

Матрица выглядит, как

$\mathbf{A} = \begin{bmatrix} \mathbf{A}_{1} & 0 & \cdots & 0 \\ 0 & \mathbf{A}_{2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \mathbf{A}_{n} \end{bmatrix}$

где каждый элемент A_k является квадратной ненулевой матрицей. Определитель квазидиагональной матрицы равен произведению определителей диагональных клеток.

Квазитреугольная матрица

Квазитреугольной называется клеточная матрица A у которой клетки A_ij = 0 при i > j (или i < j):

$\mathbf{A} = \begin{bmatrix} \mathbf{A}_{11} &amp;amp; \mathbf{A}_{12} &amp;amp; \cdots &amp;amp; \mathbf{A}_{1n} \\ 0 &amp;amp; \mathbf{A}_{22} &amp;amp; \cdots &amp;amp; \mathbf{A}_{2n} \\ \vdots &amp;amp; \vdots &amp;amp; \ddots &amp;amp; \vdots \\ 0 &amp;amp; 0 &amp;amp; \cdots &amp;amp; \mathbf{A}_{nn} \end{bmatrix}$.

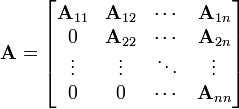Определитель квазитреугольной матрицы равен произведению определителей диагональных клеток.

Блочно-трёхдиагональная матрица

Блочно-теплицева матрица