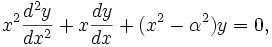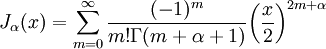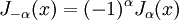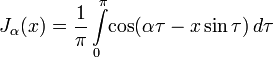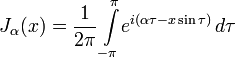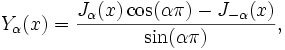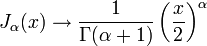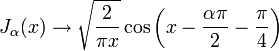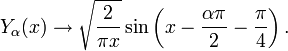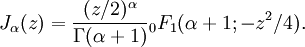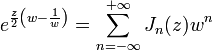Бесселевы функции

Функции Бесселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:

$x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - \alpha^2)y = 0,$

где α — произвольное действительное число, называемое порядком.

Наиболее часто используемые функции Бесселя — функции целых порядков.

Хотя α, и − α порождают одинаковые уравнения, обычно договариваются о том, чтобы им соответствовали разные функции (это делается, например, для того, чтобы функция Бесселя была гладкой по α).

Функции Бесселя впервые были определены швейцарским математиком Даниилом Бернулли, а названы в честь Фридриха Бесселя.

Применения

Уравнение Бесселя возникает во время нахождения решений уравнения Лапласа и уравнения Гельмгольца в цилиндрических и сферических координатах. Поэтому функции Бесселя применяются при решении многих задач о распространении волн, статических потенциалах и т. п., например:

• электромагнитные волны в цилиндрическом волноводе;
• теплопроводность в цилиндрических объектах;
• формы колебания тонкой круглой мембраны
• скорость частиц в цилиндре, заполненном жидкостью и вращающемся вокруг своей оси.

Функции Бесселя применяются и в решении других задач, например, при обработке сигналов.

Определения

Поскольку приведённое уравнение является уравнением второго порядка, у него должно быть два линейно независимых решения. Однако в зависимости от обстоятельств выбираются разные определения этих решений. Ниже приведены некоторые из них.

Функции Бесселя первого рода

Функциями Бесселя первого рода, обозначаемыми J_α(x), являются решения, конечные в точке x = 0 при целых или неотрицательных α. Выбор конкретной функции и её нормализации определяются её свойствами. Можно определить эти функции с помощью разложения в ряд Тейлора около нуля (или в более общий степенной ряд при нецелых α):

$J_\alpha(x) = \sum_{m=0}^\infty \frac{(-1)^m}{m! \Gamma(m+\alpha+1)} {\left({\frac{x}{2}}\right)}^{2m+\alpha}$

Здесь Γ(z) — это гамма-функция Эйлера, обобщение факториала на нецелые значения. График функции Бесселя похож на синусоиду, колебания которой затухают пропорционально 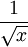$\frac{1}{\sqrt{x}}$, хотя на самом деле нули функции расположены не периодично.

Ниже приведены графики J_α(x) для α = 0,1,2:

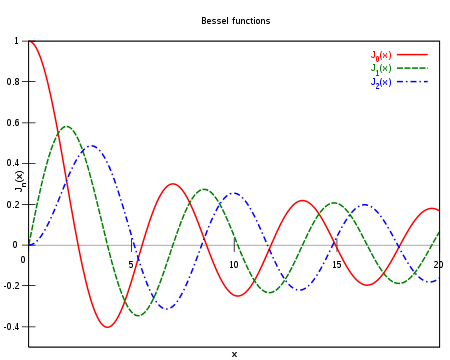
Если α не является целым числом, функции J_α(x) и J _{− α}(x) линейно независимы и, следовательно, являются решениями уравнения. Но если α целое, то верно следующее соотношение:

$J_{-\alpha}(x) = (-1)^{\alpha} J_{\alpha}(x)\,$

Оно означает, что в этом случае функции линейно зависимы. Тогда вторым решением уравнения станет функция Бесселя второго рода (см. ниже).

Интегралы Бесселя

Можно дать другое определение функции Бесселя для целых значений α, используя интегральное представление:

$J_\alpha (x) = \frac{1}{\pi} \int\limits_{0}^{\pi}\!\cos (\alpha \tau - x \sin \tau)\,d\tau$

Этот подход использовал Бессель, изучив с его помощью некоторые свойства функций. Возможно и другое интегральное представление:

$J_\alpha (x) = \frac{1}{2 \pi} \int\limits_{-\pi}^{\pi}\!e^{i(\alpha \tau - x \sin \tau)}\,d\tau$

Функции Бесселя второго рода

Функции Бесселя второго рода — решения Y_α(x) уравнения Бесселя, бесконечные в точке x = 0.

Y_α(x) также иногда называют функцией Неймана (Ньюмана) и обозначают как N_α(x). Эта функция связана с J_α(x) следующим соотношением:

$Y_\alpha(x) = \frac{J_\alpha(x) \cos(\alpha\pi) - J_{-\alpha}(x)}{\sin(\alpha\pi)},$

где в случае целого α берётся предел по α, вычисляемый, например, с помощью правила Лопиталя.

Ниже приведён график Y_α(x) для α = 0,1,2: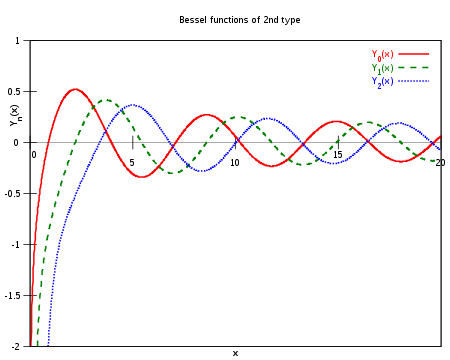

Свойства

Асимптотика

Для функций Бесселя известны асимптотические формулы. При маленьких аргументах 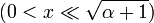$(0 < x \ll \sqrt{\alpha + 1})$ и неотрицательных α они выглядят так:

$J_\alpha(x) \rightarrow \frac{1}{\Gamma(\alpha+1)} \left( \frac{x}{2} \right) ^\alpha$

$Y_\alpha(x) \rightarrow \left\{ \begin{matrix} \frac{2}{\pi} \left[ \ln (x/2) + \gamma \right] & \mbox{;}\quad\alpha=0 \\ \\ -\frac{\Gamma(\alpha)}{\pi} \left( \frac{2}{x} \right) ^\alpha & \mbox{;}\quad\alpha > 0 \end{matrix} \right.$,

где γ — постоянная Эйлера — Маскерони (0.5772…), а Γ — гамма-функция Эйлера. Для больших аргументов (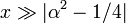$x \gg |\alpha^2 - 1/4|$) формулы выглядят так:

$J_\alpha(x) \rightarrow \sqrt{\frac{2}{\pi x}} \cos \left( x-\frac{\alpha\pi}{2} - \frac{\pi}{4} \right)$

$Y_\alpha(x) \rightarrow \sqrt{\frac{2}{\pi x}} \sin \left( x-\frac{\alpha\pi}{2} - \frac{\pi}{4} \right).$

Гипергеометрический ряд

Функции Бесселя могут быть выражены через гипергеометрическую функцию:

$J_\alpha(z)=\frac{(z/2)^\alpha}{\Gamma(\alpha+1)} {}_0F_1 (\alpha+1; -z^2/4).$

Таким образом, при целых n функция Бесселя однозначная аналитическая, а при нецелых — многозначная аналитическая.

Производящая функция

Существует представление для функций Бесселя первого рода и целого порядка через коэффициенты ряда Лорана функции определённого вида, а именно

$e^{\frac{z}{2}\left(w-\frac{1}{w}\right)}=\sum_{n=-\infty}^{+\infty}J_n(z)w^n$

См. также

• Цилиндрические функции
• Сферические функции

Литература

• Ватсон Г., «Теория бесселевых функций» т. 1,2 М., ИЛ, 1949 г.
• Бейтмен Г., Эрдейи А. «Высшие трансцендентные функции. Функции Бесселя, функции параболического цилиндра, ортогональные многочлены». Справочная математическая библиотека М. Физматгиз 1966 г. 296 с.