Теория рядов

Теория рядов

Предположим, что у нас есть бесконечная последовательность следующих чисел: 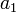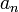$\ a_1$, $\ a_2$,.. $\ a_n$,… Тогда можно определить следующий символ: 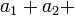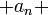$\ a_1 +a_2+$…$\ +a_n+$…=$\sum_{i=0}^\infty a_i$. Этот символ называется числовым рядом. Числовой ряд — символ, составленный из членов бесконечной числовой последовательности, соединённых формальным символом «+». Если сложить k первых членов последовательности ряда, то полученное число будет называться частичной суммы k членов данного ряда. Числовой ряд называется сходящимся, если существует предел частичных сумм при n стремящемся к бесконечности и говорят, что ряд сходится. В других случаях ряд называется расходящимся и ряд расходится.

Числовую последовательность можно задать не только перечислением членов этой последовательности, но и общей формулой, по которой можно получить член этой последовательности по его номеру n. В этом случае эта формула называется общим членом ряда и записывается перед заглавной греческой буквой «Сигма», математическим знаком суммирования, сверху и снизу которой ставятся пределы ссумирования.

Необходимым (но не достаточным) условием сходимости числового ряда является стремление общего члена к «0» при n --> бесконечности. Так, например, ряд 1+1/2+1/3+1/4+..+1/n+.. является расходящимся, несмотря на то, что общий член стремится к нулю.

Необходимым и достаточным условием сходимости числового ряда является существование верхней границы множества всех частичных сумм ряда. Супремум этого множества (или инфимум множества всех верхних границ)будет являться суммой этого ряда.

Существуют признаки сходимости числового ряда.

Так, из расходимости меньшего ряда следует расходимость большего, а из сходимости большего — сходимость меньшего. Обратное неверно.

Для определения большего и меньшего ряда достаточно сравнить n-ные члены двух рядов (Найти их отношение).

См. также

• Сумма ряда