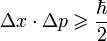Пси-функция

Квантовая механика

$\Delta x\cdot\Delta p \geqslant \frac{\hbar}{2}$

Принцип неопределённости

Введение ... Математическая формулировка ... Основа Классическая механика · Интерференция · Бра и кет · Гамильтониан Фундаментальные понятия Квантовое состояние · Волновая функция · Суперпозиция · Запутанность · Измерение · Неопределённость · Запрет Паули · Дуализм · Декогеренция · Теорема Эренфеста · Туннелирование Эксперименты Опыт Дэвиссона — Джермера · Опыт Поппера · Опыт Штерна — Герлаха · Опыт Юнга ·Проверка неравенств Белла · Фотоэффект · Эффект Комптона Формулировки Картина Шрёдингера · Картина Гейзенберга · Картина взаимодействия · Матричная квантовая механика · Интегралы по траекториям Уравнения Уравнение Шрёдингера · Уравнение Паули · Уравнение Клейна — Гордона · Уравнение Дирака Интерпретации Копенгагенская интерпретация · Теория скрытых параметров · Многомировая Сложные темы Квантовая теория поля · Квантовая гравитация · Теория всего Известные учёные Планк · Эйнштейн · Шрёдингер · Гейзенберг· Йордан · Бор · Паули · Дирак · Фок · Борн · де Бройль · Ландау · Фейнман · Бом · Эверетт

Волнова́я фу́нкция (функция состояния, пси-функция, амплитуда вероятности) — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния квантовомеханической системы, имеющей протяжённость в пространстве. В широком смысле — то же самое, что и вектор состояния.

Вариант названия «амплитуда вероятности» связан с копенгагенской интерпретацией квантовой механики: плотность вероятности нахождения частицы в данной точке пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния.

Физический смысл квадрата модуля волновой функции

Волновая функция 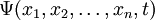$\! \Psi(x_1, x_2, \ldots , x_n,t)$ зависит от координат (или обобщённых координат) системы и, в общем случае, от времени, и формируется таким образом, чтобы квадрат её модуля 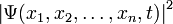$\! \left|\Psi(x_1, x_2, \ldots , x_n,t)\right|^2$ представлял собой плотность вероятности 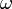$~\omega$ (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами 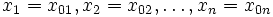$\! x_1=x_{01}, x_2=x_{02}, \ldots , x_n=x_{0n}$ в момент времени $~t$:

$~\omega = \frac{dP}{dV} = \left|\Psi(x_1, x_2, \ldots , x_n,t)\right|^2 = \Psi^\ast\Psi$.

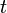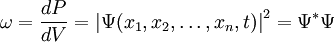Тогда в заданном квантовом состоянии системы, описываемом волновой функцией 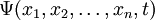$\! \Psi(x_1, x_2, \ldots , x_n,t)$, можно рассчитать вероятность 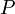$~P$ того, что частица будет обнаружена в любой области пространства конечного объема $~V$: $P={\int{dP}}={\int\limits_{V} {\omega}dV}={\int\limits_{V}{\Psi^\ast\Psi}dV}$     $~(1)$.

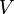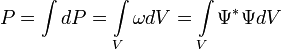
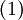Набор координат, которые выступают в роли аргументов функции, представляет собой полный набор физических величин, которые можно измерить в системе. В квантовой механике возможно выбрать несколько полных наборов величин, поэтому волновая функция одного и того же состояния может быть записана от разных аргументов. Выбранный для записи волновой функции полный набор величин определяет представление волновой функции. Так, возможны координатное представление, импульсное представление, в квантовой теории поля используется вторичное квантование и представление чисел заполнения или представление Фока и др.

Если волновая функция, например, электрона в атоме, задана в координатном представлении, то квадрат модуля волновой функции представляет собой плотность вероятности обнаружить электрон в той или иной точке пространства. Если эта же волновая функция задана в импульсном представлении, то квадрат её модуля представляет собой плотность вероятности обнаружить тот или иной импульс.

Принцип суперпозиции квантовых состояний

Основная статья: Квантовая суперпозиция

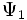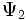Для волновых функций справедлив принцип суперпозиции, заключающийся в том, что если система может пребывать в состояниях, описываемых волновыми функциями $\! \Psi_1$ и $\! \Psi_2$, то она может пребывать и в состоянии, описываемом волновой функцией

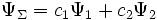$\! \Psi_\Sigma = c_1 \Psi_1 + c_2 \Psi_2$ при любых комплексных 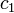$\! c_1$ и $\! c_2$.

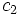Очевидно, что можно говорить и о суперпозиции (сложении) любого числа квантовых состояний, то есть о существовании квантового состояния системы, которое описывается волновой функцией $\! \Psi_\Sigma = c_1 \Psi_1 + c_2 \Psi_2 + \ldots + {c}_N{\Psi}_N=\sum_{n=1}^{N} {c}_n{\Psi}_n$.

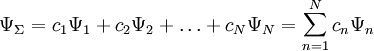В таком состоянии квадрат модуля коэффициента 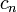$~{c}_n$ определяет вероятность того, что при измерении система будет обнаружена в состоянии, описываемом волновой функцией $~{\Psi}_n$.

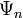Поэтому для нормированных волновых функций $~\sum_{n=1}^{N}\left|c_{n}\right|^2=1$.

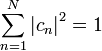Условия регулярности волновой функции

Вероятностный смысл волновой функции накладывает определенные ограничения, или условия, на волновые функции в задачах квантовой механики. Эти стандартные условия часто называют условиями регулярности волновой функции.

1. Условие конечности волновой функции. Волновая функция не может принимать бесконечных значений, таких, что интеграл 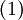$~(1)$ станет расходящимся. Следовательно, это условие требует, чтобы волновая функция была квадратично интегрируемой функцией. В частности, в задачах с нормированной волновой функцией квадрат модуля волновой функции должен стремиться к нулю на бесконечности.
2. Условие однозначности волновой функции. Волновая функция должна быть однозначной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно. В задачах с использованием цилиндрической или сферической системы координат условие однозначности приводит к периодичности волновых функций по угловым переменным.
3. Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть также частные производные волновой функции 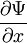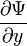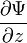$~\frac{\partial \Psi}{\partial x}$, $~\frac{\partial \Psi}{\partial y}$, $~\frac{\partial \Psi}{\partial z}$. Эти частные производные функций лишь в редких случаях задач с идеализированными силовыми полями могут терпеть разрыв в тех точках пространства, где потенциальная энергия, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода.

Свойство нормировки волновой функции

Отметим свойство нормировки волновой функции 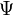$\! \Psi$ в частном случае трёхмерного пространства в декартовых координатах. В этом случае 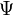$\! \Psi$ зависит от времени t и трёх переменных 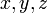$\! x, y, z$, являются решением уравнения Шрёдингера) и удовлетворяет условию нормировки:

${\iiint\limits_{-\infty}^{+\infty} {|\Psi|}^2 dx\,dy\,dz}=1$

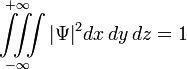
Это условие выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией во всем пространстве равна единице.

Матричная и векторная формулировки

Одна и та же волновая функция в различных представлениях — будет соответствовать выражению одного и того же вектора в разных системах координат. Остальные операции с волновыми функциями так же будут иметь аналоги на языке векторов.

Функциональная (волновая), матричная и векторная формулировки математически эквивалентны.

Философский смысл волновой функции

Волновая функция представляет собой метод описания чистого состояния квантовомеханической системы. Смешанные квантовые состояния (в квантовой статистике) следует описывать оператором типа матрицы плотности. То есть, некая обобщённая функция от двух аргументов должна описать корреляцию нахождения частицы в двух точках.

Следует понимать, что проблема, которую решает квантовая механика, — это проблема самой сути научного метода познания мира. Если представить себе бильярдный стол, закрытый непроницаемой крышкой, и единственным способом исследования вопроса, есть ли на нём бильярдные шары, предположить закатывание в стол других шаров, то мы и получаем ту самую проблему, для решения которой привлечён метод квантовой механики. Пока вброшенный шар проходит сквозь стол без изменения траектории, предсказуемо, мы можем сделать вывод о том, что на траектории шара других шаров нет. Если в результате взаимодействия шаров на столе мы получаем выкатившиеся несколько шаров с различными конечными импульсами и точками, в которых шары покинули стол, то мы можем лишь предполагать о том, каким образом происходило взаимодействие в системе. Если же лузы в бильярдном столе ограничивают возможность шаров покидать стол (энергетический барьер), то система запутывается ещё больше. Подобный пример с бильярдом очень наглядно демонстрирует те трудности, с которыми сталкиваются исследователи, разрабатывая инструменты квантовой механики.

См. также

• Собственное состояние
• Оператор (физика)
• Уравнение Шрёдингера
• Принцип неопределённости Гейзенберга
• Блоховская волна
• Редукция волновой функции
• Функция Вигнера

Литература

• Физический энциклопедический словарь./Гл. ред. А.М.Прохоров. Ред. кол. Д.М.Алексеев, А.М.Бонч-Бруевич, А.С.Боровик-Романов и др. — М.: Сов. Энциклопедия, 1984. — 944 с.

Ссылки

• Большая Советская Энциклопедия: Квантовая механика, Яндекс.Словари
• Физический энциклопедический словарь: Квантовая механика»

Разделы физики
Экспериментальная физика | Теоретическая физика
Механика | Специальная теория относительности | Общая теория относительности | Космология | Молекулярная физика | Термодинамика | Статистическая физика | Физическая кинетика | Электродинамика | Оптика | Акустика | Физика плазмы | Физика конденсированного состояния | Атомная физика | Квантовая физика | Квантовая механика | Квантовая теория поля | Ядерная физика | Физика элементарных частиц | Теория колебаний | Нелинейная динамика | Метрология | Астрофизика | Геофизика | Биофизика | Радиофизика | Материаловедение | Физика атмосферы | Химическая физика | Физическая химия | Математическая физика

	Разделы механики	п·о·р
теоретическая механика | небесная механика | квантовая механика | классическая механика | сопротивление материалов | строительная механика | теория колебаний | теория упругости | теория пластичности | теория устойчивости | теория катастроф|}