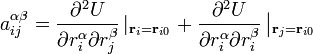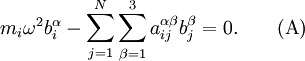- Мода (физика)
-
 Различные нормальные моды в 1D решётке.
Различные нормальные моды в 1D решётке.Нормальные колебания или нормальные моды — набор характерных для колебательной системы типов гармонических колебаний. Каждое из нормальных колебаний физической системы, например, колебаний атомов в молекулах, характеризуется своей частотой. Набор частот нормальных колебаний составляет колебательный спектр. Произвольное колебание физической системы можно представить в виде суперпозиции нормальных колебаний. Вынужденные колебания физической системы имеют резонанс на частотах, которые совпадают с частотами нормальных колебаний.
Содержание
Нормальные колебания в молекулах
Общая теория
Потенциальная энергия взаимодействия атомов в молекулах является определённой функцией их координат
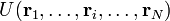 . Эта функция в целом рассчитывается из квантовой механики в адиабатическом приближении или задаётся определёнными модельными потенциалами. Равновесные положение атомов в молекулах
. Эта функция в целом рассчитывается из квантовой механики в адиабатическом приближении или задаётся определёнными модельными потенциалами. Равновесные положение атомов в молекулах 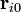 задаются условием минимума этой функции
задаются условием минимума этой функции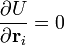 .
.
Если вывести молекулу из равновесия так, что каждый атом сместится на некую величину
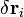 , то в молекуле возникнут силы, которые постараются вернуть атомы в положение равновесия, а потенциальна энергия возрастёт и станет равной
, то в молекуле возникнут силы, которые постараются вернуть атомы в положение равновесия, а потенциальна энергия возрастёт и станет равной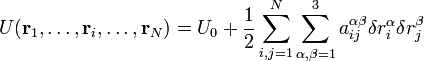 ,
,
где і и j — индексы атомов, α и β — индексы осей координат, U0 — потенциальная энергия молекуулы в положении равновесия, а коэффициенты
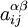 определяются разложением потенциальной энергии в ряд Тейлора в окрестности положения равновесия.
определяются разложением потенциальной энергии в ряд Тейлора в окрестности положения равновесия.Уравнения движения для смещённых из положения равновесия атомов имеют следующий вид:
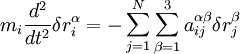 ,
,
где mi — масса i-того атома.
Если искать решения системы дифференциальных уравнений в виде
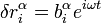 ,
,
то получим систему линейных уравнений
Всего таких уравнений 3N-6, где N — число атомов. 3 другие уравнения описывают движение центра массы молекулы, а ещё три — вращения молекулы, как целого[1] . Система однородная, а следовательно имеет нетривиальное решение лишь при определённых частотах, которые находятся, если приравнять нулю детерминант этой системы
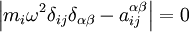 ,
,
где δij — символ Кронекера.
Данный детерминант является уравнением (3N-6)-ей степени относительно ω², которое называется вековым или секулярным уравнением. Его корни определяют спектр собственных частот колебаний молекулы.
Собственные векторы
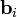 уравнения (A) определяют 3N-6 нормальных мод колебаний молекулы.
уравнения (A) определяют 3N-6 нормальных мод колебаний молекулы.Нормальные моды взаимно линейно независимы и взаимно ортогональны:
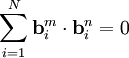 ,
,
если
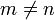 , где m и n — индексы, которыми обозначены различные собственные векторы. Именно этой особенности нормальные моды обязаны своим названием.
, где m и n — индексы, которыми обозначены различные собственные векторы. Именно этой особенности нормальные моды обязаны своим названием.Дипольный момент
Если известны нормальные моды, которые задаются векторами
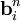 , где индекс n — номер моды, а также частичные заряды атомов в молекулах, то можно образовать векторы:
, где индекс n — номер моды, а также частичные заряды атомов в молекулах, то можно образовать векторы: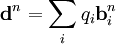 ,
,
которые называются дипольными моментами нормальных мод.
Во внешнем электрическом поле, например, в поле электромагнитной волны, энергия диполя определяется формулой
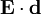 . Поэтому те нормальные моды, которые имеют значительный дипольный момент сильно взаимодействуют с электромагнитными волнами (обычно инфракрасного диапазона). Те нормальные моды, для которых дипольного момента нет, или он очень мал, не поглощают и не излучают инфракрасные волны.
. Поэтому те нормальные моды, которые имеют значительный дипольный момент сильно взаимодействуют с электромагнитными волнами (обычно инфракрасного диапазона). Те нормальные моды, для которых дипольного момента нет, или он очень мал, не поглощают и не излучают инфракрасные волны.Например, симметричная молекула O2 не имеет частичного заряда на своих атомах, поэтому кислород в атмосфере не становится препятствием для распространения инфракрасных волн. В молекуле CO2 атомы кислорода несколько подтягивают электроны к себе от центрального атома углерода, поэтому все три атомы имеют небольшой частичный заряд. В молекуле углекислого газа (она линейная) есть три нормальные моды. Одна из них — это симметричные колебания атомов кислорода вдоль оси молекулы. Эта мода не имеет дипольного момента. Другая мода колебаний — асимметричные колебания атомов кислорода вдоль оси молекулы имает дипольный момент, как и третья мода, в которой молекула сгибается.
Источники
- Федорченко А.М. . — Киев: Висшая школа, 1975., 516 с.
Примечания
- ↑ Для двухатомных молекул число уравнений равно 1, потому что вращение происходит только вокруг двух осей.
Wikimedia Foundation. 2010.