- Критерий Краскела-Уоллиса
-
Критерий Краскела-Уоллиса предназначен для проверки равенства средних нескольких выборок. Данный критерий является многомерным обобщением критерия Уилкоксона-Манна-Уитни. Критерий Краскела-Уоллиса является ранговым, поэтому он инвариантен по отношению к любому монотонному преобразованию шкалы измерения. Известен так же под названиями: критерий Крускала-Уоллиса,H-критерий Краскела-Уоллиса, Kruskal-Wallis one-way analysis of variance, Kruskal-Wallis test.
Содержание
Примеры задач
Пример 1. Проходит чемпионат мира по футболу. Первая выборка —- опрос болельщиков с вопросом «Каковы шансы на победу сборной России?» до начала чемпионата. Вторая выборка —- после первой игры, третья —- после второго матча и т. д. Значения в выборках — шансы России на победу по десятибальной шкале (1 —- никаких перспектив, 10 —- отвезти в Россию кубок —- дело времени). Требуется проверить, зависят ли результаты опросов от хода чемпионата.
Описание критерия
Заданы k выборок:
 . Объединённая выборка:
. Объединённая выборка:  .
.Дополнительные предположения:
- обе выборки простые, объединённая выборка независима;
- выборки взяты из неизвестных непрерывных распределений
 .
.
Проверяется нулевая гипотеза
 при альтернативе
при альтернативе  . Упорядочим все
. Упорядочим все 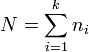 элементов выборок по возрастанию и обозначим Rij ранг j-го элемента i-й выборки в полученном вариационном ряду. Статистика критерия Краскела-Уоллиса для проверки гипотезы о наличии сдвига в параметрах положения двух сравниваемых выборок имеет вид
элементов выборок по возрастанию и обозначим Rij ранг j-го элемента i-й выборки в полученном вариационном ряду. Статистика критерия Краскела-Уоллиса для проверки гипотезы о наличии сдвига в параметрах положения двух сравниваемых выборок имеет вид  , где
, где 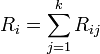 ;
; 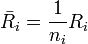 . Гипотеза сдвига отклоняется на уровне значимости α, если
. Гипотеза сдвига отклоняется на уровне значимости α, если  , где Hα — критическое значение, при
, где Hα — критическое значение, при  и
и  вычисляемое по таблицам. При больших значениях применимы различные аппроксимации.
вычисляемое по таблицам. При больших значениях применимы различные аппроксимации.Аппроксимация Краскела-Уоллиса
Пусть
 ;
;  ;
; 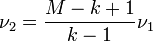 ;
; 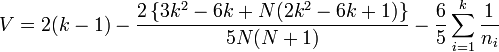 . Тогда статистика
. Тогда статистика 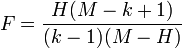 будет иметь при отсутствии сдвига F-распределение с ν1 и ν2 степенями свободы. Таким образом, нулевая гипотеза отклоняется с достоверностью α, если F > Fα(ν1,ν2).
будет иметь при отсутствии сдвига F-распределение с ν1 и ν2 степенями свободы. Таким образом, нулевая гипотеза отклоняется с достоверностью α, если F > Fα(ν1,ν2).Аппроксимация Имана-Давенпорта
В соответстви с ней нулевая гипотеза сдвига отклоняется с достоверностью α, если
 , где
, где  ;
;  , Fα(f1;f2) и
, Fα(f1;f2) и  — соответственно критические значения статистик Фишера и хи-квадрат с соответствующими степенями свободы. Это более точная аппроксимация, чем аппроксимация Краскела-Уоллиса. При наличии связанных рангов (то есть когда совпадают значения величин из разных выборок и им присваиваются одинаковые средние ранги) необходимо использовать модифицированную статистику
— соответственно критические значения статистик Фишера и хи-квадрат с соответствующими степенями свободы. Это более точная аппроксимация, чем аппроксимация Краскела-Уоллиса. При наличии связанных рангов (то есть когда совпадают значения величин из разных выборок и им присваиваются одинаковые средние ранги) необходимо использовать модифицированную статистику 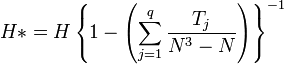 , где
, где 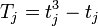 ; tj — размер j-й группы одинаковых элементов; q — количество групп одинаковых элементов. При
; tj — размер j-й группы одинаковых элементов; q — количество групп одинаковых элементов. При  справедлива аппроксимация распределения статистики H; χ2 -распределением с f=k-1 степенями свободы, то есть нулевая гипотеза отклоняется, если
справедлива аппроксимация распределения статистики H; χ2 -распределением с f=k-1 степенями свободы, то есть нулевая гипотеза отклоняется, если  .
.Литература
- Kruskal W. H. and Wallis W. A. Use of ranks in one-criterion variance analysis. // Journal of the American Statistical Association. — 1952, 47 № 260. — Pp. 583—621.
- Ликеш И., Ляга Й. Основные таблицы математической статистики. — М.: Финансы и статистика, 1985.
- Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006. — 466—468 с.
Ссылки
Wikimedia Foundation. 2010.
