2Д-система для частиц двух сортов

2Д-система для частиц двух сортов

2Д-система для частиц двух сортов (Two sorts paricles 2D-system) - стандартная квантово-механическая задача для движения частиц двух сортов (например, электронов и дырок) в замкнутой двумерной (2Д-) системе (пространственный 2Д-ящик). Стандартное определение температуры в статистической физике, основывающееся на описании движения частиц в замкнутом трехмерном (3М-) ящике ^[1], с помощью уравнения Шредингера ^[2] наталкивается на определенные трудности для двумерной (2Д-) системы, так как в этом случае предсказывается бесконечное значение температуры. В то же время практика показывает существование 2М-систем не только при больших температурах, но и при очень низких, вблизи абсолютного нуля. Поскольку для твердого тела характерен двухчастичный механизм проводимости (например, частицы и дырки), то целесообразно рассмотреть двухчастичные движения в замкнутом 2М-ящике и найти его температуру. Впервые эта задача была рассмотрена Якимахой ^[3] в конце 80-х годов при исследовании двумерных инверсионных слоев на поверхности кремния.

Квантовая теория 2М- ящика

Система стационарных уравнений Шредингера, описывающая двухчастичное движение в 2М-системе, имеет вид:

$-\frac{\hbar^2}{2m_j}[\frac{d^2\Psi_j}{dy^2}] + [\frac{d^2\Psi_j}{dz^2}] = W_j\Psi_j \$, (1)

где j = 1,2 − частицы двух сортов, Ψ_j − волновая функция:

$\Psi_j = A_{0j}\exp [i(yk_{yj} + zk_{zj}] \$,

где m_j − масса j − й частицы, $\hbar = \frac{h}{2\pi}$ - приведенная постоянная Планка, k_j − волновой вектор. Для ограниченного 2М-объема 0 < y < L;0 < z < L − нормировка волновой функции $\Psi_J(0) = \Psi_J(L) = 0 \$ налагает следующие ограничения на значения волновых векторов:

$(k_{yj} + k_{zj})L = \pi (n_{yj} + n_{zj}) = \pi l \$ (2)

где $l = n_{yj} + n_{zj} = 1,2,... \$ Можно получить общее решение системы уравнений (1)

$W_j = W_{0j}\pi (n_{yj}^2 + n_{zj}^2, \$ (3)

$W_{0j} = \frac{(\frac{h}{L})^2}{8\pi m_j} \$. (4)

Радиусы 2М-сфер двухчастичных состояний можно записать в виде:

$R_j = \sqrt{n_{yj}^2 + n_{zj}^2} = \sqrt{\frac{W_j}{\pi W_{0j}}}$

а число состояний для каждой из частиц в интервале энергий от 0 до W_j составляет:

$\Phi_j = 2[\frac{\pi R_j^2}{4}] = \frac{W_j}{2W_{0j}}$,

здесь учтено, что обе частицы принадлежат классу ферми-частиц. Полное число состояний частиц обеих сортов в 2М-системе имеет вид:

$\Phi_{\Sigma} = \Phi_1 \cdot \Phi_2 = \frac{W_1W_2}{4W_{01}W_{02}}$ (5)

В силу сложившейся традиции, обычно рассматривают состояния (5) на квазинепрерывном участке, когда $W_j \gg W_{0j}$ ^[1]. Поэтому целесообразно рассмотреть противоположный случай, когда значения энергии (3) находятся вблизи основного состояния (4). При таком рассмотрении возникает естественная нормировка выражения (5):

$\Phi_j = 1, \$

приводящая к «замкнутости двухчастичных состояний 2М-системы, запертой в 2М-ящике, а также к соотношению

$W_j = 2W_{0j}. \$ (6)

Последнее выражение означает, что полная энергия двухчастичных состояний $W(2) \$ равна удвоенному значению энергии одночастичных состояний $W(1) \$:

$W_j(2) = 2W_j(1) = 2W_{0j} \$.

Число состояний в интервале энергий от $W_j \$ до $W_j + \delta W_j\$ составлдяет величину:

$\Omega_j = \frac{d\Phi_{\Sigma}}{dW_j}\cdot \delta W_j, \$

а суммарное число двухчастичных состояний в интервале энергий от $W_j \$ до $W_j + \delta W_j\$-

$\Omega_{\Sigma} = \Omega_1\cdot \Omega_2 = \frac{W_1W_2\delta W_1\delta W_2}{16(W_{01}W_{02})^2} \$. (7)

Будучи последовательными, необходимо и здесь применить нормировку замкнутости двухчастичных состояний 2М-системы:

$\Omega_{\Sigma} = 1 \$, (8)

из которой с учетом (6) и (8) находим соотношение:

$\delta W_j = 2W_{0j}, \$

то есть минимальные порции энергии в основном состоянии также дискретные и определяются энергией этого состояния.

Значение (8) для Ω_Σ приводит к равенству нулю энтропии замкнутых двухчастичных состояний в 2М-ящике

$S_{2D} = k_B\ln \Omega_{\Sigma} = 0, \$

где $k_B - \$ постоянная Больцмана. Последнее выражение предполагает, что сформированная указанным способом двухчастичная система представляет собой квантовый объект макроскопических размеров ($L - \$ параметр длины). В тоже время температура здесь принимает дискретные значения:

$T_j = \frac{\Omega_{\Sigma}}{k_B}\cdot \frac{dW_j}{d\Omega_{\Sigma}} = \frac{W_j}{k_B} = (\frac{h}{L})^2\frac{1}{8\pi k_Bm_j}$ (9)

причем температура двухчастичных состояний равна T_j(2) = 2W_0j / k_B,одночастичных состояний двухчастичной системы - T_j(1) = W_0j / k_B. Здесь можно отметить, что необходимым условием для проявления макроскопических квантовых явлений является требование превышения кванта температуры (9) над температурой среды, окружающей 2М-ящик.

Плотность одночастичных состояний и концентрации частиц

Плотность одночастичных состояний N_j(W_j) (где j = 1,2 − частицы двух сортов) 2М-системы может быть выражена через полное число состояний в диапазоне энергий от $W_j \$ до $W_j + \delta W_j\$:

$\Omega_{\Sigma} = \Omega_1\cdot \Omega_2 = \frac{W_1W_2\delta W_1\delta W_2}{16(W_{01}W_{02})^2} = N_1(W_1)N_2(W_2)L^4\delta W_2\delta W_2 .$ (10)

Для случая N₁ = N − 2 (всегда выполняется на практике), имеем:

$N_j = \frac{W_j}{4W_{0j}^2L^2}. \$

Одночастичная концентрация носителей тока одного из сортов частиц 2М-системы может быть представлена (для W_j = 2W_0j) в виде:

$n_j(W) = \int_{W}^{} \delta (W - 2W_{0j}N_j(W)F(W)dW\, dW = F(W)L^{-2}. \$ (11)

где $\delta (W) - \$ дельта функция Дирака, $F(W) - \$ функция распределения Ферми-Дирака. Из этого выражения следует, что 2М-плотность одночастичных состояний равна $N_{j2D}^* = L^{-2} \$. Учет третьего измерения, которое ограничивает толщину 2М-системы (L_x), приводит к значению трехмерной плотности:

$N_{j2D}^* = \frac{1}{L_xL^2} = L^{-3}$.

Здесь третье измерение вводится для того, чтобы подчеркнуть что 2М-система в реальном случае находится внутри полноценной 3М-системы (случай кремния), а не просто в вакууме изолирована. Поскольку энергия замкнутого двухчастичного состояния связана с областью ограничения 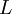$L \$ выражением вида (4), то задавая величину $W_{0j} \$ постоянной, найдем значение длины:

$L = \frac{h}{\sqrt{8\pi m_j W_{0j}}} = \frac{h}{\sqrt{8\pi m_jk_BT_{0j}}}$ (12)

где $T_{0j} \$ берем из (9). Как известно ^[4], выражение типа (12) выполняет роль тепловой длины волны де Бройля. Таким образом, трехмерную плотность состояний можно представить в виде:

$N_{j3D}^* = 8[\frac{2\pi m_jk_BT}{h^2}]^{3/2}$

которая практически совпадает с общепринятой (с точностью до числового коэффициента) для борновского приближения модели зонной структуры полупроводника. Если в 2М-системе выполняется распределение Максвелла-Больцмана ^[4]:

$F(W) = \exp (\frac{W - W_g}{k_BT}) \$,

где $W_F - \$ энергия Ферми, то концентрация частиц (электронов и дырок) может быть представлена в виде:

$n = N_{3D}^*\exp [\frac{W_F - W_c}{k_BT}]$ (13a)

$p = N_{3D}^*\exp [\frac{W_v - W_F}{k_BT}]$, (13b)

где $W_c, W_v - \$ соответственно нижний уровень зоны проводимости и верхний уровень валентной зоны.

Но основной особенностью 2М-системы частиц двух сортов в твердом теле является наличие только двух уровней с энергией $W_c, W_v \$ (при отсутствии самой зонной структуры), причем разница этих энергий и определяет ширину запрещенной зоны $W_g \$ (энергетическую щель), которая равна энергии основного состояния одночастичных состояний:

$W_g = W_c - W_v = W_{0j} \$.

Ширина запрещенной зоны связана с собственной концентрацией 2М-системы соотношением

$n_i = N_{3D}^* \exp (-\frac{W_g}{2k_BT}) \$.

Здесь необходимо отметить, что 2М-система будет хорошо проявлять свои свойства лишь в том случае, когда ширина запрещенной зоны «индуцированной 2М-системы» близка к ширине запрещенной зоны в объеме полупроводника (например, в кремнии). Полагая

$W_g = W_{0j} = 1,082715 \$еВ

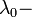при $L_1 = \lambda_0/\alpha \$, где $\lambda_0 - \$ комптоновская длина волны электрона, 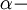$\alpha - \$ постоянная тонкой структуры, а 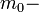$m_0 - \$ масса свободного электрона, находим значение «собственной трехмерной концентрации 2М-системы в 3М-системе:

$n_{i3D} = 5,272198 \cdot 10^{13} \$ 1/см ³. (14)

Трансцендентное уравнение (14) можно решить относительно температуры методом последовательных приближений

$T_c = T_c(n_{i3D} = 419,8336 K \$, (15)

где T_c − критическое значение температуры фазового перехода из 2М- в 2М-состояние.

Концентрация частиц в истинно двумерной системе

В отличие от кремния, где двухчастичная 2М-система электронов и дырок как бы «плавает» в 3М-пространстве полупроводника (вернее возле ее поверхности), также могут существовать и полностью изолированные двухчастичные системы, которые по умолчанию лишены третьего измерения. Примером такой 2М-системы может выступать графен. Очевидно, что и в этом случае будут справедливы соотношения для концентраций носителей типа (13), только в этом случае здесь необходимо использовать двумерное значение концентраций:

$N_{2D}^* = \frac{8\pi m^*k_BT}{h^2} \$.

Здесь также можно ввести т.н. уровень энергии для средины запрещенной зоны

$W_i = \frac{W_c + W_v}{2}$,

который соответствует собственной концентрации 2М-полупроводника при отсутствии примесей:

$n_{i2D} = N_{2D}^* \exp (\frac{-W_g}{2k_BT}) \$. (16)

Если предположить, что и в случае идеальной 2М-системы мы также будем иметь то же значение для собственной концентрации (14), тогда путем несложных преобразований находим 2М-значение для собственной концентрации, равное

$n_{i2D} \approx 3,03 \cdot 10^{14}$ 1/м ², (17)

которое весьма близко к реальному минимальному значению концентрации, достижимой в графене, правда при этом значения критической температуры и ширины запрещенной зоны станут другими.

Ширина запрещенной зоны в истинно двумерной системе

Ширина запрещенной зоны в идеальной 2М-системе определяет собственную концентрацию двумерной системы:

$n_{i2D} = \frac{8\pi m^*k_B}{h^2}\cdot T_c\cdot \exp (\frac{-W_g}{2k_BT_c})$, (18)

где $T_c \$ значение критической температуры 2М-системы. Если предположить, что и здесь также соблюдается значения критической температуры, что и для «плавающей» 2М-системы в 3М-пространстве полупроводника, равное $T_c = 419,83 K \$, тогда приняв в качестве оценки для минимального значения эффективной массы носителей тока значение $m^* = \alpha m_0 \$, можно определить «температуру» запрещенной зоны:

$T_g = W_g/k_B = 1666,76 K \$,

которая соответствует ширине запрещенной зоны:

$W_g = T_gk_B = 0,144 \$ эВ.

Безусловно это достаточно большое значение ширины запрещенной зоны, хотя и значительно меньше, чем в кремнии. Если оно до сих пор не обнаружено экспериментально, так его просто никто и не искал. Его можно определить путем исследования экситонов в графене или путем облучения лучами вблизи этой энергии. Опять следует отметить, что это ширина «индуцированной» запрещенной зоны в графене, и она не имеет никакого отношения к реальной (металлургической) зонной структуре графита или графена. То, что она в углероде проявляется, говорит лишь о ее близости к металлургической зонной структуре графита.

Экспериметальное подтверждение наличия критической температуры

Наличие термостабильной точки в различных кремниевых полупроводниковых приборах, равное $T_c \approx 420 K \$, подтверждено в конце 80-х годов Якимахой ^[3]. То, что она имела непосредственное отношение к фазовому переходу подчеркивал тот факт, что при превышении температуры выше 420К сама «температуростабильная точка» исчезала, а ВАХ приборов также менялась (ток стока эквидистантно смещался при увеличении затворного напражения или напряжения на базе). При этом использовались не только серийные МДП- транзисторы типов КП301Б, КП304А, работающие в полевом режиме, но также измерялись они и в «биполярном режиме» (подложка исполняла роль базы, а затвор заземлялся). Более того, исследовались также и p-n-переходы (сток-затворные и исток- затворные), а также и маломощные планарные биполярные транзисторы КТ363Б, КТ203, КТ316. Самым удивительным было то, что традиционно считающиеся объемнопроводящими биполярные транзисторы и p-n-переходы также проявляли двумерный характер проводимости.

См. также

Квантовая емкость (графен)

Примечания

1. ↑ ^{1 2} Рейф Ф. Статистическая физика. Учебное руководство/Пер. с англ.; Под ред. А.И.Шальникова и А.О.Вайсенберга.- 3-е изд., испр. – М.:Наука, 1986.-336с.
2. ↑ Ансельм А.И. Очерки развития физической теории в первой трети 20-го века.-М.:Наука, 1986.-248с.
3. ↑ ^{1 2} Якимаха А.Л. Высокотемпературные квантовые гальваномагнитные эффекты в двумерных инверсионных слоях МДП-транзисторов. Киев: Выща школа, 1989, - 91с. ISBN 5-11-002309-3 djvu
4. ↑ ^{1 2} Бонч-Бруевич В.Л., Калашников С.Г. Физика полупроводников. М.:Наука, 1977.-672с.